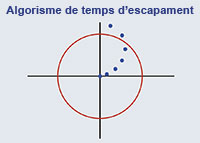
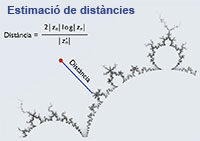
Volcano, por Javier Barrallo. Aunque las imágenes fractales se crean típicamente con un aspecto bidimensional, es posible simular una imagen con aspecto tridimensional utilizando algunos efectos de programación. Esencialmente, se calcula una «altura» para cada punto basándose en un determinado algoritmo de color. Después se define un plano tangente a la superficie y un vector normal a ésta, lo cual determina de forma realista la cantidad de luz y de sombra que se tiene que administrar a cada punto. Fractal Geometry: Algorithms and Artistic Creation. With the increasing complexity of fractal generation software, the focus of exploration in new fractal techniques is shifting away from fractal formulas and towards colouring algorithms. This paper provides an overview of colouring algorithms in popular use and a general classification system for these techniques in fractal art creation. Las imagenes fractales Los sistemas dinámicos son una de las ramas de las matemáticas más desarrolladas hoy en día, pero hasta la llegada de los ordenadores, el elevado número de cálculos que implicaba su uso los hacían impracticables en la vida real. Actualmente, la capacidad del ordenador para efectuar operaciones a gran velocidad permite condensar millones de cálculos en resultados que podemos interpretar numérica o visualmente. Benoit Mandelbrot fue el primero en utilizar los ordenadores para producir representaciones gráficas de sistemas dinámicos en el plano complejo, basándose en las fórmulas descritas por el matemático francés Gastón Julia a principio de siglo. Durante la década de los 80, los primeros estudiosos de los fractales comenzaron a explorarlos por su valor estético, más que por su significación matemática. Mientras que la matemática era la herramienta, el objetivo era el arte. Al ser las ecuaciones fractales el elemento matemático más obvio, los artistas fractales experimentaron con nuevas ecuaciones, introduciendo centenares de nuevos tipos fractales. Eligiendo cuidadosamente parámetros para refinar el color, la forma y el encuadre, estos pioneros introdujeron el concepto de arte fractal. Después de 1995, prácticamente se había agotado la posibilidad de crear nuevos tipos fractales de especial relevancia. Entonces la mayor innovación se produce no al cambiar las ecuaciones fractales, sino al crear nuevas formas de colorear las ecuaciones ya existentes. A medida que estos nuevos algoritmos de coloreado se hacen más complejos, los artistas fractales regresan a las ecuaciones fractales más simples y clásicas, ya que la flexibilidad de estos sofisticados algoritmos de color proporciona, por sí misma, una mayor versatilidad y posibilidad de expresión artística personal. Algoritmos de color Cada sistema dinámico produce una secuencia de valores z0, z1, z2, z3,… zn. Las imágenes fractales se crean generando una de estas secuencias para cada píxel (punto de la pantalla) en la imagen. Posteriormente, el algoritmo de color es el encargado de interpretar la secuencia numérica para producir un color final que la represente. The eyes of the beholders (Los ojos de los vigilantes) por Domenik Anuzzi. Esta imagen constituye un ejemplo de cómo el uso de diferentes capas puede ser utilizado para buscar y resaltar una determinada forma o efecto. Típicamente, el algoritmo de color produce un único valor para cada píxel. Dado que el color es interpretado en los ordenadores como un espacio tridimensional RGB (red, green, blue), este valor unidimensional debe ser expandido para poder producir un color. El método más común es la creación de una paleta, una secuencia de valores de color 3D, definidos por una línea (denominada gradiente) que recorre el espacio tridimensional. La selección del gradiente es una de las decisiones artísticas más críticas al crear una imagen fractal. Un gradiente de color puede enfatizar partes de la imagen u ocultar otras. En casos extremos, dos imágenes fractales con los mismos parámetros pero diferentes esquemas de color pueden parecer completamente diferentes. Podemos efectuar una primera división entre los algoritmos de color: los que producen valores discretos y los que producen valores continuos. Los valores discretos muestran saltos o bandas en la transición del color. Hasta hace unos años esto no era importante, ya que las tarjetas gráficas de 8 bits producían, en cualquier caso, un escalonado en la imagen. Sin embargo la llegada masiva de las tarjetas gráficas de 24 bits hizo que los algoritmos continuos cobraran una especial preponderancia, ya que permiten interpolar un color cualquiera del gradiente con la precisión deseada. La creciente importancia de los algoritmos de color en las imágenes fractales ha dado lugar a centenares de nuevos algoritmos, de entre los que podemos destacar los que se detallan a continuación. Algoritmo de tiempo de escape El algoritmo de tiempo de escape es uno de los más antiguos y para muchos programas fractales la única opción disponible. Su simplicidad lo convierte en el favorito de aquellos que se inician en la programación fractal, sin embargo, desde el punto de vista artístico se considera menos importante, dado que produce valores discretos y se ha visto ampliamente superado por los algoritmos de color continuos. Este algoritmo está basado en el número de iteraciones necesario para determinar si la secuencia iterada por el sistema dinámico tiende a infinito o no. Puede demostrarse estrictamente que, cuando la órbita de cualquier valor z0, z1, z2, z3,… zn excede una región frontera, R siempre diverge hacia el infinito. La forma y el tamaño mínimo de la región R son, por supuesto, diferentes para cada fórmula fractal. La secuencia iterada es interrumpida tan pronto como zn rebasa la región frontera R, entonces el valor de coloreado para el algoritmo de tiempo de escape es simplemente la longitud de la secuencia, esto es n. Tradicionalmente, R se define como un círculo, centrado en el origen y con radio 2. Esto viene dado porque en el conjunto de Mandelbrot está probado que tan pronto como |z|>2 la iteración diverge. Y aunque matemáticamente R debe incluir un círculo de radio 2 para verificar la divergencia de forma precisa, esto no ha impedido a algunos artistas fractales experimentar con otros radios diferentes. El algoritmo de tiempo de escape puede ser considerado como una medida no euclídea de la distancia de un punto cualquiera z0 a la frontera del conjunto. El uso de un valor discreto (el número de iteraciones es siempre un entero) produce una apariencia de bandas similar a la de un mapa topográfico. El uso creativo de los gradientes puede en algún caso sacar provecho de estas bandas (también denominadas “rayado de tigre”) pero la mayoría de los artistas han desarrollado algoritmos que ocultan este efecto. Claramente, el objetivo final es crear funciones continuas para medir estas distancias. Aunque los algoritmos empleados no proporcionan una distancia euclidiana exacta, sí que proporcionan una aproximación aceptable utilizando valores continuos. No todas las secuencias iteradas z0, z1, z2, z3,… zn tienden hacia infinito. Las órbitas que no lo hacen, a menudo convergen en un solo punto o en un ciclo periódico. Aunque la mayoría de las técnicas descritas anteriormente pueden aplicarse a estas secuencias convergentes, requieren de ciertas modificaciones. El método más sencillo consiste en buscar un cambio decreciente en la órbita de zn. Así, mientras zn converge hacia un punto fijo, |zn–zn-1| tiende hacia cero. Una vez que esta diferencia rebasa una tolerancia establecida, consideramos que el punto ha convergido suficientemente hacia el atractor y lo coloreamos (puede ser de acuerdo al número de iteraciones o a cualquier otro algoritmo). Ángulo de escape Los algoritmos descritos anteriormente consideraban la magnitud de z y el número de iteraciones. Si consideramos la magnitud z como una parte de las coordenadas polares de zn, entonces parece lógico considerar también la otra parte –el ángulo de z– como elemento para colorear. La familia de algoritmos de ángulo de escape cubre todos aquellos algoritmos basados en el estudio del ángulo de zn. El primer algoritmo sería la descomposición binaria. En este algoritmo, los valores de zn que toman ángulos por encima del eje real (0-180º) toman un determinado color, mientras que los que toman valores por debajo del eje real (180-360º) toman otro radicalmente diferente. Variaciones del esquema de la descomposición binaria pueden incrementar el número de divisiones del plano. Por ejemplo, una descomposición cuaternaria podría asignar un color diferente a los ángulos de zn correspondientes a cada cuadrante. El incremento del número de divisiones del plano incrementa, lógicamente, el número de colores a emplear. Otro aspecto de la secuencia z0, z1, z2, z3,… zn que puede ser medido es la curvatura entre iteraciones consecutivas. Una estimación rápida puede hacerse utilizando dos puntos de la iteración. Otras variantes permiten utilizar el radio de la circunferencia que pasa por los valores de tres iteraciones o el área del triángulo formado por tres iteraciones. Estas últimas variantes recogen no sólo la curvatura de las iteraciones, sino también la distancia entre ellas.
Captura de órbitas Constituye sin duda la más amplia familia de algoritmos de color, dada la gran versatilidad que muestra para la expresión artística. La idea básica consiste en elegir una región del plano complejo (denotada por T) y estudiar la relación entre los valores de zn y T. La región T es definida usualmente como una forma (generalmente de cálculo simple como un punto, línea o círculo) y una distancia de tolerancia. Cualquier iteración que caiga dentro de la distancia de tolerancia se considera “capturada”. Las implementaciones primitivas del algoritmo de captura de órbitas simplemente buscaban cualquier zn que cayera dentro de la región T, también denominada “trampa”. Cuando se daba esta circunstancia se concluía la iteración y se coloreaba el píxel de acuerdo a la distancia al centro de la región T. De ahí el término “trampa”; una vez que la órbita cae en T, ésta es “atrapada” y la iteración finalizada. Existen muchas variantes para este método. En primer lugar, la forma de la región T puede variar y transformarse en figuras más complejas como elípses, astroides, hipérbolas, curvas trigonométricas o curvas polares como espirales o cardioides. Más lejos aún, estas trampas pueden distorsionarse o rotarse, incluso incrementar su área con cada iteración. Otro tipo de variantes trata la relación entre las distancias de cada valor zn respecto a T. La implementación clásica, mencionada anteriormente, se detenía cuando un valor zn caía dentro de la distancia de tolerancia T. Pero otras variantes pueden utilizar el último valor zn en caer en la trampa, o el más cercano, o el más lejano, etc. E incluso métodos más exóticos pueden combinar varias de estas distancias simultáneamente, hasta el punto de hacer casi imposible predecir qué tipo de resultados se obtendrán. Una variante de la captura de órbitas es el algoritmo de enteros gaussianos. Un entero gaussiano es un número complejo cuyas componentes real e imaginaria son ambas números enteros. El algoritmo calcula la distancia de cada zn al entero gaussiano más cercano, y entonces se colorea basándose en la distancia menor obtenida en la iteración. Fractales multicapa Hoy en día la técnica más relevante de creación artística consiste en combinar simultáneamente varios algoritmos como los descritos anteriormente. El resultado final es un algoritmo mixto de enorme complejidad pero que genera imágenes de gran belleza, que denominamos fractales multicapa y que constituyen la vanguardia del arte fractal moderno. Las posibilidades de combinación son prácticamente infinitas y amplían a límites insospechados el campo de expresión artística. Esta nueva técnica dio lugar a que varios artistas fractales se unieran en una exposición itinerante denominada “The Frontier between Art and Science”, que ha sido presentada hasta el momento en España, Francia, Japón, Austria, Yugoslavia, Alemania, Argentina, Brasil y Bélgica con obras de gran formato realizadas por Linda Allison, Sylvie Gallet, Damien Jones, Mario Markus, Janet Parke, Kerry Mitchell, Michael Field, Domenick Anuzzi, Iñigo Quilez, Klaus-Peter Kubik, Luke Plant, Javier Barrallo, Mark Townsend, Earl Hinrichs y Sharon Webb. Referencias Javier Barrallo Calonge. ETS Arquitectura. Universidad del País Vasco. |
«La mayor innovación artística no se produce buscando nuevas ecuaciones fractales, sino creando nuevas formas de colorear las ya existentes»
«En casos extremos dos mimágenes fractales con las mismas fórmulas y parámetros, pero diferentes esquemas de color, pueden parecer completamente diferentes»
Taupensky, por Janet Parke. El movimiento browniano, el movimiento pseudocaótico que se produce en las partículas de polvo suspendido en el aire o en alguna turbia, ha sido transportado al campo de los algoritmos de color con gran éxito. Gracias a este efecto se consiguen tramas de gran realismo que son profusamente utilizadas como fondo de las imágenes o como texturas del motivo principal.
La exposición “The Frontier between Art and Science” ha sido presentada en España, Francia, Japón, Austria, Yugoslavia, Alemania, Argentina, Brasil y Bélgica. |