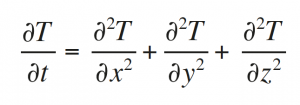La conjetura de Hodge

La conjetura de Hodge es uno de los siete problemas del milenio, y se enmarca en las áreas de la geometría diferencial y la geometría algebraica. Fue propuesto por William Hodge en 1950, y está sirviendo de estímulo para el desarrollo de diversas teorías que tienen sus fuentes en la geometría, el análisis y la física matemática. Plantea una condición natural para la existencia de subvariedades complejas dentro de una variedad compleja. Las variedades son los espacios en los que se pueden considerar objetos geométricos. En las variedades complejas el espacio tiene una estructura basada en los números complejos, en vez de la estructura más intuitiva de la geometría basada en los números reales.

Palabras clave: geometría compleja, topología, homología, teoría de Hodge, variedades.

Divulgar matemáticas

Hoy en día las matemáticas se han convertido en un área altamente tecnificada, con multitud de disciplinas y subdisciplinas. El lenguaje que se usa en la investigación matemática es enormemente abstracto. Por este motivo, cuando un matemático se enfrenta a la tarea de explicar un problema al gran público se da cuenta del abismo entre lo que se entiende comúnmente por matemáticas y la forma de trabajar del investigador. No obstante, los matemáticos sabemos de la importancia de dar a conocer los avances más reseñables y de transmitirlos con el lenguaje más cercano posible. Es por esto que se celebran congresos con proyección mediática, se otorgan distinciones a matemáticos que han logrado grandes avances y se proponen premios por la resolución de problemas concretos. Los siete problemas del milenio son un buen ejemplo. No son problemas para el común de los mortales, pero marcan unas posibles direcciones de trabajo importantes para el futuro, si bien se podrían haber planteado otros problemas igual de relevantes. Tampoco se espera ningún plazo especial para resolverlos («del milenio» hace referencia a la entrada del nuevo milenio, no a que deban estar un milenio sin resolver). Lo más reseñable es que sirven para espolear el avance científico, son el tipo de problemas que fomentan el desarrollo de nuevas teorías, y eso es lo que los hace tan valiosos.

«La topología es la rama de las matemáticas que se dedica a buscar propiedades de los espacios que pueden servir para determinar su forma»

La conjetura de Hodge es el quinto problema de los propuestos por el Instituto Clay de Matemáticas. Es un problema del área de geometría (más precisamente, en términos matemáticos, de geometría diferencial y de geometría algebraica). El problema fue originalmente propuesto por el matemático escocés William Hodge durante el Congreso Internacional de Matemáticos que tuvo lugar en el año 1950 en Cambridge, Massachussets, Estados Unidos (Hodge, 1950). Estos congresos se celebran cada cuatro años y suponen el mayor evento dentro de las matemáticas, destinados a poner al día las distintas corrientes y los hallazgos más recientes, así como a entregar las importantes medallas Fields. Hodge era conferenciante plenario, y en su conferencia expuso la reciente –para la época– teoría de formas armónicas para el estudio de la topología de las variedades diferenciables y complejas, hoy en día conocida como teoría de Hodge. También propuso extender un resultado natural de representabilidad de clases de homología con subvariedades en variedades diferenciables al caso de variedades complejas.

(Izquierda) Dos espacios que se pueden obtener uno a partir del otro por una deformación reversible sin rupturas se consideran iguales. En la imagen observamos la deformación de un donut en una taza. Topológicamente son el mismo espacio. / Núria Server (Derecha) Cada región de una superficie puede dibujarse en un mapa bidimensional que puede ser cuadriculado. En la imagen, una superficie y un mapa de esta. / V. Muñoz

El lector podrá contar el número de palabras que le resultan extrañas en el último párrafo para darse cuenta del nivel de sofisticación en que se encuentra la matemática actual. Pasemos a introducir los conceptos mencionados para hacer entendible el enunciado.

Geometría diferencial

La geometría es el área de las matemáticas que se ocupa de estudiar los espacios geométricos y los espacios físicos, así como las figuras (objetos) y sus interacciones en estos espacios. El nacimiento de la geometría se remonta al antiguo Egipto y experimentó un desarrollo muy importante en la antigua Grecia. Los libros de geometría de Euclides son probablemente la obra matemática más famosa de la historia. En ellos se describían las formas básicas del plano y el espacio (puntos, rectas, polígonos) y sus interacciones (movimientos, intersecciones). Posteriormente, la geometría también pasó a ocuparse de formas curvas (curvas, superficies), y experimentó un desarrollo paralelo al del análisis matemático. Isaac Newton desarrolló el concepto de la derivada de una función para definir el vector tangente a una curva. El concepto más revolucionario surgió con el término de variedad diferenciable, introducido por Bernhard Riemann en el siglo xix, que es el objeto central de la geometría diferencial. Una variedad diferenciable es un espacio que localmente (en un entorno de cada punto en el que nos situemos) parece un espacio euclidiano de cierta dimensión n. La superficie terrestre es un buen ejemplo en dimensión 2. Cada región de una superficie puede dibujarse en un mapa bidimensional que puede ser cuadriculado. Un lugar en la Tierra se corresponde con una posición (x, y) de ese mapa. Obviamente estos mapas se solapan, y las coordenadas dependen del mapa, pero podemos viajar por toda la superficie si tenemos el atlas completo de todos los mapas que la cubren.

«La conjetura de Hodge es un problema de geometría diferencial y de geometría algebraica»

El gran paso de la geometría, que ya venía gestándose desde siglos atrás con las dudas sobre la inmodificabilidad de los postulados de la geometría de Euclides (lo que acabaría dando pie a las geometrías no euclídeas), consistió en darse cuenta de que esta propiedad local no obligaba a todo el espacio a ser ℝⁿ. Para los no matemáticos, ℝ es la recta de los números reales (cada posición la marca un número real), y ℝⁿ es el producto de n rectas reales en n direcciones independientes. Por tanto, ℝ² es un plano (con dos ejes coordenados) y ℝ³ es el espacio (con tres ejes coordenados). Claramente, aunque al situarnos sobre la superficie terrestre nos parezca ver un plano a nuestro alrededor, la forma global de la Tierra no es la de un plano. Un ejemplo más claro es el de nuestro universo, que es una variedad diferenciable de dimensión 3 (obviamos aquí el tiempo, y la noción de espacio-tiempo, para simplificar la exposición). Localmente el universo se puede cartografiar con tres coordenadas, pero globalmente (en su totalidad) podría tener cualquier forma que escapa a nuestra imaginación. Los geómetras hemos desarrollado numerosas maneras de entender y de «ver» espacios de tres y más dimensiones.

Un hecho importante es que en una variedad diferenciable se puede diferenciar (derivar), y esto permite escribir cualquier problema en el que intervengan ecuaciones diferenciales (como la teoría de la gravedad de Newton o la teoría de la relatividad de Einstein). A eso se debe el calificativo de «diferenciable» que le otorgamos.

Topología y homología

Para clasificar las variedades necesitamos ciertas propiedades matemáticas que las distingan. Estas son las propiedades globales (llamadas así porque las variedades son todas localmente iguales, solo en su globalidad se diferencian). ¿Por qué una esfera y la superficie de un donut –un toro, en matemáticas– son distintas? Aquí hay que formalizar con mucho cuidado el concepto de «ser distinto» y «ser igual» (con palabras matemáticas como «difeomorfas»). Dos espacios que se pueden obtener uno a partir de otro por una deformación reversible sin roturas se consideran iguales. Esto se debe a que ambos tienen atlas equivalentes, es decir, los mismos mapas, cambiando las escalas de las distancias según las deformaciones, valen para ambos.

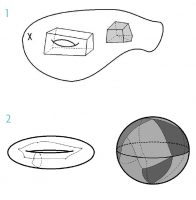
1) A l’esquerra, un forat de dimensió k = 2 en una varietat X. A la dreta, un forat fictici. 2) A l’esquerra, forats 1-dimensionals en el tor. A la dreta, el forat 2-dimensional de l’esfera rodejat per un 2-poliedre curvilini que tapa tota l’esfera.

Las propiedades más destacables que han servido para distinguir variedades diferenciables entre ellas son las conocidas como propiedades topológicas. La topología es la rama de las matemáticas que se dedica a buscar propiedades de los espacios que pueden servir para determinar su forma. Es un área relativamente reciente, cuyos orígenes se remontan a Leonhard Euler, con su famosa resolución del problema de los puentes de Königsberg, pero que tiene su nacimiento oficial a principios del siglo xx con Henri Poincaré. Un concepto importante en topología es el de homología (Poincaré, 1895). La homología de un espacio cuenta sus agujeros. La esfera y el toro son distintos porque tienen distinto número de agujeros (y, de hecho, distinto «tipo» de agujeros). Intuitivamente, un agujero es «algo que le falta» al espacio, pero el espacio es todo lo que tenemos a nuestra disposición y no podemos recurrir a nada fuera de él, porque el espacio no está en ninguna parte ni hay nada fuera (piense el lector en nuestro universo). La solución al problema consiste en buscar el agujero en el espacio rodeándolo con un objeto (se suele usar un poliedro por convención). De hecho, se define agujero k-dimensional como un poliedro de dimensión k, y se eliminan aquellos k-poliedros que se puedan poner como el borde de un poliedro (k + 1)–dimensional, en cuyo caso, de hecho, no hay agujero (sería un agujero ficticio).

Por ejemplo, en el caso del toro tenemos agujeros 1-dimensionales dados por poligonales que rodean al toro en dos direcciones. La esfera no tiene estos agujeros 1-dimensionales, pero tiene un agujero 2-dimensional que se rodea tapando toda la esfera. Los k-poliedros son topológicos, es decir, no debemos pensarlos como rectilíneos.

«La teoría de Hodge establece un nexo entre análisis matemático y topología»

Los agujeros se pueden sumar formalmente, para lo que ponemos coeficientes a las caras de los poliedros. La idea consiste en que 2 veces un ciclo es equivalente a ponerlo dos veces, una muy cerca de otra. También se puede pensar en que lo ponemos con cierto «peso». Este peso (el coeficiente asignado al ciclo) puede finalmente ser tomado negativo, o un número racional como 3/2, o incluso un número real. Cuando hablamos de homología con coeficientes racionales queremos decir que permitimos multiplicar los ciclos por un coeficiente racional.

Un resultado muy importante de René Thom, por el que le otorgaron la Medalla Fields en 1958, establece que todo agujero k-dimensional puede determinarse o «rodearse» por una subvariedad de dimensión k. Una subvariedad es una variedad metida dentro de la variedad ambiente X, para lo cual su dimensión k ha de ser menor que la dimensión n de X. El resultado de Thom tiene la particularidad de que precisa que se usen coeficientes racionales para la homología. Como ejemplo, podemos pensar en el caso del toro. Los agujeros 1-dimensionales de este pueden darse por subvariedades de dimensión 1, es decir, por curvas (en vez de por poligonales).

Teoría de Hodge

La teoría de Hodge pone en relación las formas armónicas con los elementos de la homología, es decir, establece un nexo entre análisis matemático y topología. Para entenderlo, pensemos en lo que ocurre cuando tenemos una unidad de calor en un punto del espacio. Este se disipa distribuyéndose por todo el espacio siguiendo la conocida como ecuación del calor, que tiene la siguiente forma en el espacio tridimensional (t es el tiempo y T la temperatura):

La distribución de temperatura final corresponde al caso estático (cuando ya no hay transferencia de calor dentro del espacio), y está determinada por la ecuación:

que se llama ecuación del laplaciano (en honor a ­Pierre-Simon Laplace). A sus soluciones se las denomina funciones armónicas. Para un espacio n-dimensional, tendremos que poner más coordenadas. Las k-subvariedades también se «disipan» por un proceso similar. Para entenderlo tenemos que cambiar las funciones por las k-formas. Una k-forma es un objeto matemático que se puede integrar en una k-variedad, igual que una función se evalúa en un punto (nótese que un punto es una 0-variedad). Por ejemplo, la integral usual en ℝ³ se denota como ∫ f (x, y, z)dx dy dz, y la expresión dx dy dz es un ejemplo de una 3-forma.

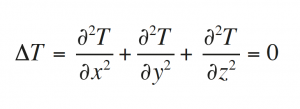
«Cuando cambiamos los números reales por Números complejos muchas propiedades matemáticas se simplifican y se vuelven más uniformes»

La potente teoría de Hodge dice que toda clase de homología (en una n-variedad cerrada, finita y sin borde) viene dada por una única forma armónica, siguiendo el proceso de disipación análogo al de la ecuación del calor. Para ello hace falta usar coeficientes reales en la homología. Por tanto, los agujeros de una variedad vienen determinados por soluciones a una ecuación en derivadas parciales de un tipo muy especial (que se denomina ecuaciones elípticas, y son ecuaciones con numerosas y muy buenas propiedades analíticas, que se estudian en profundidad en el área de ecuaciones en derivadas parciales).

En el Congrés Internacional de Matemàtics celebrat el 1950 a Cambridge, William Hodge va exposar la teoria de formes harmòniques per a l’estudi de la topologia de les varietats diferenciables i complexes, a hores d’ara coneguda com a teoria de Hodge. / John J. O’Connor & Edmund F. Robertson

Geometría compleja

El siguiente paso de complejidad en la abstracción nos lleva a usar los números complejos (¡valga la redundancia!). Estos números se denotan por C y son de la forma z = x + iy, con x, y números reales e  la unidad imaginaria. Es importante tener en cuenta que cada número complejo depende de dos números reales. En los números reales, todos los cuadrados son positivos, y por tanto la ecuación x² = –1 no tiene solución. La unidad imaginaria i es un símbolo que se añade artificialmente y que cumple la propiedad i² = –1. Es una tónica general que cuando cambiamos los números reales por números complejos muchas propiedades matemáticas se simplifican y se tornan más uniformes. Recuérdese el teorema fundamental del álgebra (demostrado por Carl Friedrich Gauss), que dice que toda ecuación polinómica siempre tiene soluciones en los números complejos, aunque no las tenga en los reales (es sorprendente que, al añadir la solución de una ecuación, todas las ecuaciones polinomiales pasen a tener soluciones). En física también es común introducir los números complejos para entender procesos del mundo real, como el estudio del electromagnetismo. En geometría no iba a ser diferente. Así C² denota el espacio complejo bidimensional, aquél que viene determinado por dos coordenadas complejas (z₁, z₂). Escribiendo z₁ = x₁ + iy₁ y z₂ = x₂ + iy₂, se deduce que cada punto de C² viene determinado por cuatro coordenadas reales (x₁, y₁, x₂, y₂); es decir, pasamos a estar en un espacio real de dimensión 4. Análogamente, C³ denota el espacio complejo tridimensional, que tiene 6 dimensiones reales. En general, dado un espacio complejo E, la dimensión real de E es el doble de su dimensión compleja. Una variedad compleja X es aquella variedad diferenciable cuyas coordenadas (locales) son números complejos. En las variedades complejas se pierde la intuición espacial porque, con el cambio de dimensiones, no podemos asimilarlas a curvas o superficies en el espacio real tridimensional.

Las variedades complejas más estudiadas son aquéllas que se pueden definir como el lugar del espacio C^N en el que un conjunto de polinomios se anulan (más precisamente, el lugar del espacio proyectivo complejo, para que obtengamos variedades cerradas y sin borde, pero mejor no entrar en más tecnicismos). Estas variedades se denominan variedades proyectivas y son el centro de atención de la geometría algebraica. Al venir determinadas por polinomios, toda la maquinaria del álgebra puede usarse para obtener sus propiedades (¡incluidas propiedades topológicas!). La confluencia de multitud de ideas, teorías y argumentos en esta área es una de esas características que confieren su belleza a las matemáticas.

«Una conjetura es una pregunta que de alguna forma se cree que ha de ser cierta, aunque no se sabe cómo demostrarla»

Una operación básica de los números complejos es la de obtener el conjugado. Si z = x + iy, entonces su conjugado es z– = x − iy (solo se ha cambiado un signo). Al considerar formas diferenciables en una variedad compleja con coordenadas (locales) (z₁, z₂…, z_n), las hay que dependen de variables z (se escriben dz₁, dz₂…, dz_n) y las hay que dependen de las variables conjugadas z– (se escriben dz–₁, dz–₂…, dz–_n), pero también las hay mixtas, que dependen en unos casos de una variable y en otros de variables conjugadas (por ejemplo: dz₁ dz–₂ dz–₃ que combina un término complejo y dos conjugados). En general, tenemos las formas de tipo (p, q), con p + q = k, que contienen p términos complejos y q términos conjugados. Por ejemplo, dz₁ dz–₂ dz–₃ es una (1,2)-forma en una variedad compleja de dimensión 3 (¡y de dimensión real 6, si el lector no se ha perdido aún!). Resolviendo la ecuación armónica para las (p, q)-formas, tenemos las (p, q)-formas armónicas y, como ya hemos indicado, también los elementos de homología de grado (p, q); es decir, los agujeros de la variedad que, al ser compleja, tienen dimensiones que son en parte complejas y en parte conjugadas (en realidad, p dimensiones complejas y q dimensiones conjugadas). Ahora hay que usar coeficientes complejos en la homología (permitiendo a los ciclos ser multiplicados por números complejos). Es una consecuencia realmente profunda que en una variedad compleja cada agujero de dimensión k tiene una dimensión compleja p y una dimensión conjugada q con k = p + q.

Se comprueba que si una clase de homología está representada por una subvariedad compleja de dimensión p (y por tanto su dimensión real es 2p), entonces es de tipo (p, p). En otras palabras, su dimensión compleja y conjugada están compensadas. Por tanto, las subvariedades complejas representan agujeros (elementos de la homología) que son racionales (de hecho, enteros) y de tipo (p, p).

La importancia del problema

Una conjetura es una pregunta que de alguna forma se cree que ha de ser cierta, aunque no se sabe cómo demostrarla. Por eso los contraejemplos, construcciones que desdicen un enunciado, son tan impactantes. Sin embargo, Hodge no planteó su pregunta como una conjetura, y tampoco hay acuerdo en si la conjetura será cierta o falsa. Las opiniones entre los matemáticos están muy divididas entre los que creen que se podrá probar, y los que creen que es falsa. El matemático André Weil (1980) propuso una 4-variedad compleja como posible contraejemplo, que aún está por dirimir. Esto destaca sobre otras conjeturas, como la hipótesis de Riemann (que también aparece entre los problemas del milenio), en las que todo el mundo cree que serán ciertas.

Enunciamos una versión moderna, ya simplificada con el tiempo, y que tiene en cuenta que enunciados ligeramente similares tienen contraejemplos (Grothendieck, 1969; Voisin, 2002). Por ejemplo, la versión con coeficientes enteros es falsa (Atiyah y Hirzebruch, 1962). En todo caso, Hodge no fue muy preciso en su pregunta, al fin y al cabo estaba meramente intentando motivar la investigación en la dirección de la teoría de Hodge y las variedades complejas.

La conjetura quedaría enunciada así: Si X es una variedad proyectiva, toda clase de homología racional y de grado (p, p) se puede representar por subvariedades complejas de dimensión compleja p. El enunciado se plantea como una extensión al resultado de Thom mencionado antes, en el que toda clase de homología racional de grado k se puede representar por una subvariedad (real obviamente, que es cuando no se especifica) de dimensión k. En este caso, las subvariedades son diferenciables, es decir, no necesariamente dadas por ecuaciones polinomiales.

«La importancia de un problema se muestra en la cantidad de teorías que ha dejado como rastro antes de ser resuelto»

La conjetura de Hodge es difícil porque las subvariedades complejas son objetos muy rígidos (al estar definidas por polinomios). De hecho es muy difícil construir subvariedades complejas y suele haber pocas. Demostrar que existen subvariedades sin construirlas (un tipo de razonamiento indirecto muy socorrido) también se ha mostrado difícil. El hecho de que el problema pertenece a una zona de confluencia de la geometría algebraica, la geometría diferencial y el análisis matemático –por no mencionar las conexiones con la geometría aritmética o con la física matemática, a las que no hemos aludido en estas líneas– hace de este problema una fuente inagotable de interacciones. De hecho, la importancia de un problema se muestra en la cantidad de teorías que ha dejado como rastro antes de ser resuelto. Estas teorías son las que perdurarán y abrirán nuevas líneas de investigación, y servirán para plantear nuevas preguntas para el siguiente milenio.