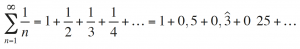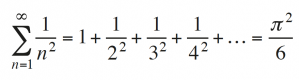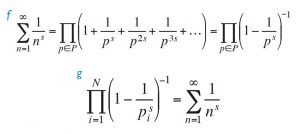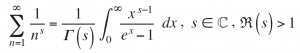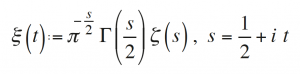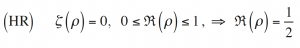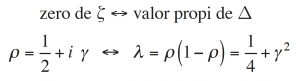La hipótesis de Riemann

La hipótesis de Riemann es una afirmación, no demostrada, que hace referencia a los ceros de la función zeta de Riemann. Bernhard Riemann calculó los seis primeros ceros no triviales de esta función y observó que todos estaban sobre una misma recta. En una memoria publicada en 1859, Riemann comentó que este podría muy bien tratarse de un hecho general. La hipótesis de Riemann afirma que todos los ceros no triviales de la función zeta se encuentran en la recta x = 1/2. Más de diez billones de ceros calculados hasta hoy, todos alineados sobre la recta crítica, corroboran la sospecha de Riemann, pero nadie aún ha podido probar que la función zeta no tenga ceros no triviales fuera de esta recta.

Palabras clave: números primos, función zeta, función L, hipótesis de Riemann, problemas del milenio.

Origen del problema

La hipótesis de Riemann es una afirmación, todavía no probada, referida a la función ζ(s), llamada «función zeta de Riemann». No es difícil demostrar que la función zeta se anula en los enteros negativos pares: ζ(-2m) = 0, para m ≥ 1, por lo que estos números se llaman «ceros triviales». Bernhard Riemann (1826- 1866) calculó seis ceros más de la función zeta, y observó que todos tenían parte real igual a 1/2: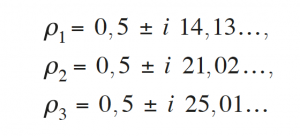En una memoria de 1859, Riemann comentó que este podría muy bien tratarse de un hecho general, aunque él no sabía cómo justificarlo. La hipótesis de Riemann presupone que todos los ceros no triviales de la función zeta se sitúan en la recta x = 1/2, denominada «recta crítica».

El interés de la localización de los ceros de la función zeta de Riemann fue destacado por el matemático alemán David Hilbert, en 1900, en el problema octavo de su lista de veintitrés problemas abiertos que presentó en el Congreso Internacional de Matemáticos, celebrado en París al inicio del pasado siglo. En el decurso de los años, se ha ido poniendo de relieve que la función zeta interviene en muchos problemas aritméticos, por lo que una demostración de la hipótesis de Riemann confirmaría la validez de gran cantidad de resultados numéricos que dependen de esta afirmación. En particular, la función zeta es, de lejos, la herramienta analítica más importante para estudiar los números primos.

«La funció zeta és, de lluny, l’eina analítica més important per a l’estudi dels nombres primers»

Más de diez billones de ceros de la función zeta calculados hasta hoy con la ayuda de los ordenadores, todos alineados en la recta crítica, hacen patente la extraordinaria intuición de Riemann. Al mismo tiempo, numerosas investigaciones sobre este tema, insuficientes hasta ahora para alcanzar el resultado final, alertan de la enorme dificultad de la cuestión. Al incluir la hipótesis de Riemann en la lista de los siete problemas del milenio, el Instituto Clay se ha hecho eco de un problema centenario y actual al mismo tiempo (Bombieri, 2000; Sarnak, 2005).

La serie armónica y los números primos

Para introducir la función zeta de Riemann es útil considerar primero la serie armónica, que se obtiene al sumar los inversos de todos los números naturales:

Los conceptos de media aritmética, media geométrica y media armónica de dos números fueron ya formulados por los pitagóricos.

La media armónica h(a,b) de dos números se define como el inverso de la media aritmética de sus inversos (a). El nombre serie armónica obedece a que cada uno de los términos es la media armónica de los dos términos contiguos (b). La serie armónica es una serie divergente, es decir, sus sumas parciales se pueden hacer tan grandes como se quiera. El erudito medieval Nicolás Oresme (1323- 1382) observó este hecho y en el texto Quaestiones super geometriam Euclidis (Oresme, 1961) le dio la demostración siguiente: es evidente que (c) y también que las agrupaciones de términos (d) son todas más grandes que 1/2, y así indefinidamente; por tanto, (e).

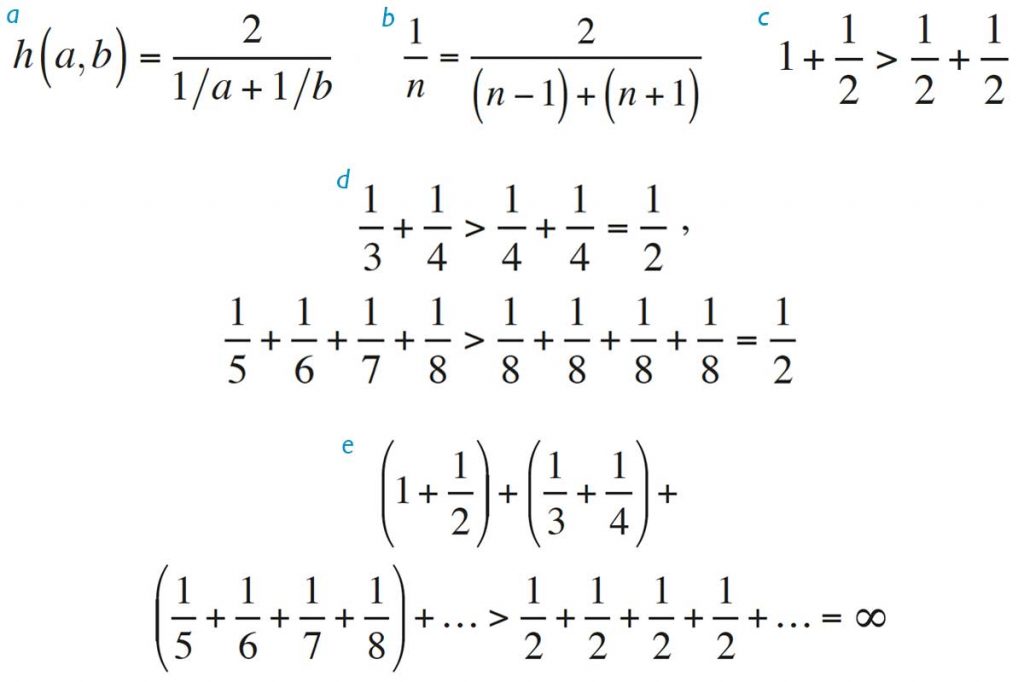
Posteriormente, el matemático Pietro Mengoli (1626- 1686), catedrático de aritmética de la Universidad de Bolonia, se interesó por la suma de los inversos de los cuadrados de los números naturales y sospechó que esta podría tratarse de una serie convergente, dado que se suman cantidades mucho más pequeñas. Leonhard Euler (1707-1783) proporcionó su valor exacto:

Al sustituir en la serie el exponente 2 por un número real s cualquiera, se obtiene una serie convergente para todos los valores s > 1, que también fue evaluada por Euler en todos los enteros positivos pares; en estos números, los valores de la función zeta se expresan como potencias del número π y en función de los llamados números de Bernoulli, que son números racionales. Desde el principio se vio que la serie así obtenida proporcionaba información sobre los números primos y que estudiarla permitiría ir más allá del conocimiento que de estos números pudieron adquirir los griegos. A partir de la suma de la serie geométrica de razón 1/ps, Euler obtuvo el producto infinito (f) donde el símbolo P denota el conjunto de todos los números primos. Euler utilizó la descomposición anterior para dar la siguiente demostración, alternativa a una dada en su día por Euclides, de la infinitud del conjunto de los números primos. Supongamos que el conjunto P = {p1,…, pN} fuese finito. Tendríamos que (g).

Sin embargo, para s = 1, el término de la izquierda representaría una cantidad finita, mientras que el de la derecha, tal como hemos visto, representaría una cantidad infinita. Por reductio ad absurdum obtenemos, pues, que P es un conjunto infinito.

En 1859 Bernhard Riemann (1826-1866), en la izquierda, fue elegido miembro de la Academia de Ciencias de Berlín. Su memoria de ingreso estaba dedicada a las leyes que rigen la distribución de los números primos. En la imagen, retrato del matemático alemán. La conjetura de Hilbert-Pólya ha dado lugar a varias interpretaciones físicas y artísticas de la hipótesis de Riemann. En el centro, el matemático alemán David Hilbert (1862-1943). A la derecha, el húngaro George Pólya (1887-1985). / Smithsonian Institution, Mètode

Euler ya advirtió –y cualquiera puede darse cuenta de ello– que los números primos se comportan de forma misteriosa: no hay ninguna fórmula que permita calcular directamente el enésimo primo pn y, obtenido este, no se conoce su distancia al primo siguiente pn + 1 (Montgomery, 1973). Ello conllevó que las primeras cuestiones en el estudio de los números primos se dirigiesen a la obtención de fórmulas que proporcionasen de forma aproximada cuántos primos π(x) hay por debajo de una cantidad dada cuando x tiende al infinito. Por ejemplo, se tiene que hasta cien hay veinticinco números primos; hasta mil hay 168; hasta un millón hay 78.498, etc., pero no disponemos de ninguna fórmula explícita que proporcione el valor π(x) de una forma exacta para cualquier valor x.

Al observar extensas tablas de primos, Carl Friedrich Gauss (1777-1855) conjeturó que π(x) ~ Li(x) cuando x → ∞, donde la función (h) denota el logaritmo integral. La conjetura es equivalente a la fórmula asimptótica (i). La prueba de esta conjetura constituyó el teorema de los números primos, que fue demostrado por primera vez en 1896 por Jacques Hadamard (1865-1963) y Charles Jean de la Vallée-Poussin (1866-1962), de forma independiente el uno del otro. Previamente, sin embargo, hay que destacar la aportación fundamental de Riemann en este campo.

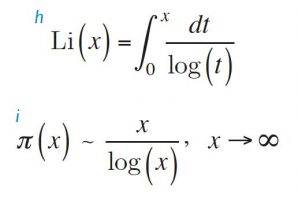
La función zeta de Riemann

En 1859, Riemann fue elegido miembro de la Academia de Ciencias de Berlín. Como memoria de ingreso, presentó el estudio Über die Anzahl der Primzahlen unter einer gegebenen Grösse (“Sobre la cantidad de números primos por debajo de una cantidad dada”) (Riemann, 1859). La memoria, cuyo manuscrito no llega a las seis páginas, puso de manifiesto que las leyes que rigen la distribución de los números primos dependen en gran parte del comportamiento de la serie armónica cuando esta se extiende a una función de variable compleja. Dado un número complejo s = x + iy, representaremos por R(s) = x, I(s) = y sus partes real e imaginaria, respectivamente, y representaremos por ℂ el conjunto de todos los números complejos.

Consideremos la función de variable compleja definida por:

En la fórmula, Γ(s) representa la función gamma que interpola el factorial, otra creación típicamente euleriana. La serie anterior converge en el semiplano R(s) > 1, pero la representación integral de la función que define permite hacer la prolongación analítica a todo el plano complejo. La función así obtenida es la función zeta de Riemann, ζ(s), que tan solo toma el valor infinito en s = 1, donde la serie armónica hemos visto que diverge. De hecho, el comportamiento de ζ(s) para R(s) < 0 está determinado por el comportamiento de ζ(s) para R(s) > 1. Los valores de ζ(s) que aportan más información son los situados en la llamada banda crítica, definida por 0 ≤ R(s) ≤ 1. El eje de simetría de la banda crítica es la recta R(s) = 1/2, denominada la recta crítica. Al evaluar la función zeta en los enteros negativos, se obtienen fórmulas equivalentes a las de Euler y, en particular, se obtiene que ζ(–2m) = 0, para todo m ≥ 1; por eso los enteros negativos pares son los llamados ceros triviales de la función zeta.

Riemann estableció que la función zeta tiene infinitos ceros en la banda crítica, y dio una estimación del número de ceros de altura acotada. Escribimos, de acuerdo con Riemann:

En Riemann (1859) encontramos el siguiente comentario sobre los ceros de ξ(t):

[…]es muy probable que todas las raíces sean reales. Por supuesto que sería deseable tener una demostración rigurosa; sin embargo, tras algunos intentos huidizos realizados en vano, he desestimado la búsqueda de una prueba de este tipo, dado que este hecho parecía prescindible para el objetivo inmediato de mi investigación.

Se conoce como hipótesis de Riemann (HR) la afirmación de que todos los ceros no triviales de la función zeta de Riemann se encuentran en la recta crítica:

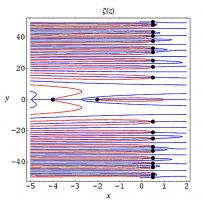
La figura 1 representa las curvas de nivel de los ceros de las partes real (en rojo) e imaginaria (en azul) de ζ(s). Los ceros, representados por un punto negro, se encuentran donde las dos curvas se cortan. Se pueden ver los dos primeros ceros triviales y los diez primeros ceros no triviales y sus simétricos, todos estos sobre la recta crítica.

El resultado central obtenido por Riemann en su memoria es una fórmula asintótica para el cálculo de π (x) que permite conectar la cantidad de primos inferiores a una cantidad dada con los ceros de la función zeta: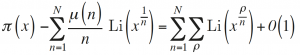donde μ(n) denota la función de Möbius, definida según μ(n) = (–1)k, si n es producto de k ≥ 0 primos diferentes y μ(n) = 0, por otra parte.

Figura 1. Primeros ceros de la función zeta de Riemann.

La fórmula de Riemann contiene tres tipos de términos: a) Términos que no crecen cuando x crece: incluidos en 0(1); b) términos que crecen cuando x crece: Li (x1/n); y c) términos que crecen en valor absoluto cuando x crece, pero que oscilan en signo: Li (xp/n). Riemann designó con el nombre de «periódicos» los términos oscilatorios e interpretó que son los causantes de las fluctuaciones observadas experimentalmente en la cantidad de primos contenidos en los diferentes intervalos (Du Sautoy, 2003; Montgomery, 1973).

La memoria de Riemann ejerció y continúa ejerciendo una influencia muy remarcable. Jacques Hadamard afirmó que había necesitado tres décadas para comprender su contenido y que había podido demostrar todas las afirmaciones de Riemann, salvo una: la hipótesis de Riemann. En 1914, Godfrey Harold Hardy (1877-1947) demostró que la función ξ(t) tiene infinitos ceros reales; equivalentemente, que la función zeta de Riemann tiene infinitos ceros en la recta crítica.

La conjetura de Hilbert-Pólya

La llamada conjetura de Hilbert-Pólya parte de una creencia popular. Propone una interpretación espectral de los ceros no triviales de la función zeta de Riemann; es decir, debería existir un operador lineal Δ cuyos valores propios se relacionasen con los ceros no triviales de la función zeta tal como se indica:

El operador Δ sería positivo y se escribiría como Δ = D(1 – D), siendo i(D – 1/2) un operador lineal autoadjunto, con lo cual el conocimiento que se tiene de estos operadores permitiría afirmar que sus valores propios γ serían números reales y la hipótesis de Riemann quedaría demostrada.

Se dice que Hilbert llamó «espectro» al conjunto de los valores propios de un operador por analogía con las líneas espectrales producidas por las frecuencias de radiación de los átomos. Más adelante, la mecánica cuántica confirmaría esta interpretación: las líneas espectrales se corresponden con vectores propios de operadores hermíticos (los cuales extienden en el campo complejo las propiedades de las matrices reales simétricas) aportados por el hamiltoniano de sistemas mecánicos-cuánticos. Recordemos que Max Born (1882-1970), Werner Heisenberg (1901-1976) y John von Neumann (1903-1957) fueron alumnos de Hilbert en Gotinga.

La conjetura de Hilbert-Pólya ha dado lugar a varias interpretaciones físicas y artísticas de la hipótesis de Riemann. Por ejemplo, el hecho de que podamos calcular el espectro de un operador que desconocemos se ha comparado al hecho de escuchar una música y no saber qué instrumento la interpreta.

La demostración de la hipótesis de Riemann podría tener también consecuencias en disciplinas como el análisis matemático o la teo-ría de la información.

Las funciones zeta de Hasse-Weil

La interpretación espectral de los ceros de la función zeta ha resultado cierta en un contexto muy diferente: para ciertas funciones zeta surgidas del estudio de sistemas de ecuaciones polinómicas. A toda variedad algebraica X, proyectiva y lisa, definida sobre el cuerpo finito de q = pf elementos se le puede asociar una función zeta de variable compleja, ζ(X,s) que atiende al número de puntos de la variedad o número de soluciones del sistema que la define. El hecho más importante es que los puntos de estas variedades pueden ser interpretados como puntos fijos de un operador, en este caso conocido, llamado «automorfismo» de Frobenius. La función es la llamada «función zeta de Hasse-Weil» y es una función mucho más sencilla que la función zeta de Riemann. Eso es porque se trata de una función racional en q–s y sus ceros –que son en número finito– satisfacen un análogo a la hipótesis de Riemann. Las aportaciones principales en este campo se deben a Emil Artin (1898-1962), Helmut Hasse (1898-1979), André Weil (1906-1998), Alexander Grothendieck (1928-2014) y Pierre Deligne, entre muchos otros. La hipótesis de Riemann en el contexto de las variedades algebraicas sobre cuerpos finitos fue probada por Deligne en los años setenta.

Epílogo

La función zeta de Riemann es una herramienta matemática creada en los siglos xviii y xix en la que el análisis de variable compleja tiene un papel importante. La finalidad principal fue, en principio, tener conocimiento del comportamiento de los números primos. La función zeta de Riemann es básica para entender la distribución de estos números, pero un resultado muy preciso relativo a la posición de los ceros de esta función falta aún por demostrar: la hipótesis de Riemann. Probarla implicaría disponer de leyes asintóticas mucho más precisas en el campo de la teoría analítica de números; leyes que, hoy por hoy, son únicamente conjeturales. Además, la demostración de la hipótesis de Riemann podría tener también consecuencias en otras disciplinas como en análisis matemático o en teoría de la información. Así, la resolución de este problema implicaría automáticamente la de muchos otros que se relacionan con él, lo cual justifica con creces la dotación económica de un millón de dólares con la que está premiado.

Durante el siglo xix se empezó a ver que el modelo proporcionado por la función zeta de Riemann para el estudio aritmético de los números enteros se podía extender al estudio aritmético de los números algebraicos; nacían así las funciones zeta de Dedekind, las funciones L de Dirichlet y, ya en el siglo xx, las funciones L de Artin y las de Hecke. El siglo xx vio asimismo la extensión de las funciones zeta y de las funciones L al estudio de las variedades definidas sobre cuerpos finitos, que hemos tratado antes. Pero la historia no se detiene aquí. La función zeta de Riemann ha sido el modelo de muchas otras funciones, conocidas también como funciones zeta y como funciones L, cuyo estudio conforma una buena parte de los retos planteados en la matemática del siglo XXI.

Tabla 1. Recopilación de funciones zeta y funciones L, el ámbito al que pertenecen y algunas de sus propiedades más notables. Las letras HR denotan que la afirmación análoga a la hipótesis de Riemann ha sido probada en el contexto correspondiente. Fuente: Pilar Bayer, 2006. 

En la tabla 1 ofrecemos una selección de objetos matemáticos que tienen asociada una función zeta o una función L. Algunas de las entradas de la tabla 1 constituyen extensísimos campos y programas de investigación actuales, como las funciones agrupadas bajo el nombre de funciones L automorfas, que conforman el profundo y extenso programa de Langlands, el cual propone una visión altamente unificadora del mundo diofántico. Los lectores interesados en ampliar esta información pueden consultar, entre muchas otras, las referencias Bayer y Neukirch, 1978; Berry y Keating, 1999; Du Sautoy, 2003; Euler, 1737; Lagarias y Odlyzko, 1987; Riemann, 1859; en el caso aritmético. En el caso aritmético-geométrico, Deligne, 1974; Weil, 1949. Para las funciones L espectrales, Connes, 1999; Katz y Sarnak, 1999; Odlyzko, 2001 y Selberg, 1956. Y para las relativas a sistemas dinámicos: Deninger, 1998; Lapidus y Van Frankenhuysen, 2001.

Tal como hemos visto, muchos objetos matemáticos tie-nen asociadas funciones zeta. De forma heterodoxa, pode-mos interpretar las funciones zeta como el ADN de estos objetos, dada la cantidad de información que aportan. Es necesario, sin embargo, saberla extraer y gestionar.