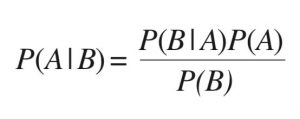La teoría que nunca murió

La regla de Bayes, una teoría sencilla del siglo XVII para la evaluación de conocimiento, fue criticada durante la mayor parte del siglo XX, pero utilizada por el Reino Unido y los Estados Unidos durante la Segunda Guerra Mundial y la Guerra Fría. Palomares y Valencia tuvieron papeles importantes en su desarrollo durante aquellos tiempos sombríos. El uso de la regla está muy extendido hoy en día en el ámbito de la computación y en muchas otras aplicaciones. Por ejemplo, Bayes se ha convertido en la clave política para la toma de decisiones basadas en datos. La revolución bayesiana ha resultado ser un cambio de paradigma moderno para una era eminentemente pragmática.

Palabras clave: regla de Bayes, Fisher, frecuentistas, Laplace.

Recientemente, una simple teoría matemática descubierta por dos clérigos británicos (Bayes, 1763) en el siglo XVIII ha tomado por asalto el mundo moderno, dominado por los ordenadores. De hecho, es una parte tan generalizada de nuestras vidas informatizadas que se ha convertido en algo chic –incluso políticamente correcto– en algunos sectores importantes de los Estados Unidos.

Sin embargo, durante la mayor parte del siglo XX fue tan controvertida que muchos de los que la utilizaban no se atrevían siquiera a mencionarla. Durante el período más tormentoso de la historia de la regla de Bayes, dos lugares en España –Palomares y Valencia– desempeñaron un papel vital para mantener viva la teoría.

De simple, la teoría resulta casi ridícula. Ayuda a la gente a evaluar sus ideas iniciales, actualizarlas y modificarlas con nueva información y a tomar mejores decisiones. En resumen, la regla de Bayes es muy breve y sencilla: Creencias iniciales + datos objetivos recientes = Una nueva creencia mejorada.

Como el ilustre economista británico John Maynard Keynes dijo con sorna, «Cuando los hechos cambian, cambio de opinión. ¿Y usted qué hace usted, señor?»

Durante el siglo XVIII, dos clérigos y matemáticos aficionados, el inglés Thomas Bayes y su amigo galés Richard Price, descubrieron y publicaron el teorema, y el matemático francés Pierre-Simon Laplace lo desarrolló en la forma en que se usa hoy en día. Ahora podríamos llamarlo la teoría Bayes-Price-Laplace, o BPL para abreviar.

La teoría es muy robusta. En la práctica, la regla de Bayes requiere múltiples cálculos, y potentes ordenadores que reintegran millones de veces la probabilidad de una creencia inicial cada vez que llega información nueva. La regla de Bayes no genera una respuesta absolutamente cierta, exacta. En cambio, utiliza la probabilidad para moverse paso a paso hacia la conclusión más probable. Sin embargo, gracias a Bayes, podemos filtrar correo basura, evaluar riesgos médicos o de otro tipo, buscar las páginas que nos interesan en Internet y descubrir lo que quizás nos interesaría comprar, basándonos en lo que hemos buscado en el pasado. El ejército lo usa para mejorar las imágenes generadas durante el vuelo de los drones, y los médicos, para mejorar nuestras resonancias magnéticas y estudios PET. Se utiliza en Wall Street, en astronomía y en física, en traducción automática de lenguas extranjeras, genética y bioinformática. La lista no acaba.

«Una simple teoría matemática descubierta por dos clérigos británicos en el siglo XVIII ha tomado por asalto el mundo moderno, dominado por los ordenadores»

Prueba A del poder actual de la regla de Bayes: encontrar objetos perdidos en el mar. Durante la Guerra Fría, la Fuerza Aérea de los Estados Unidos perdió una bomba de hidrógeno en la costa de Palomares, y la Marina de los Estados Unidos comenzó a desarrollar la teoría bayesiana en secreto para encontrar objetos bajo el agua. En 2009, el vuelo 447 de Air France desapareció en el océano Atlántico Sur con 228 personas a bordo. La Marina de los Estados Unidos había desarrollado la teoría de búsqueda bayesiana lo suficiente como para acabar con dos años de búsqueda infructuosa del AF447 en una semana de búsqueda submarina. Los expertos en búsqueda bayesiana esperan que la teoría también ayude a encontrar el vuelo 370 de Malaysian Airlines.

Para la prueba B del poder de Bayes, el coche sin conductor de Google, que comienza a rodar con la información de mapas de ruta y de las condiciones de la carretera. A medida que el automóvil se mueve en entornos de tráfico, los sensores llevan encima sobre el vehículo recogen nuevos datos de tráfico para actualizar la información inicial y calcular cuál es probablemente la conducción más segura en ese momento.

La prueba C del poder actual de Bayes tiene que ver con los filtros de correo basura. Mucha gente, incluida yo misma, recuerda comenzar el trabajo de cada día sorteando anuncios de Viagra. Por suerte, eso cambió cuando en el año 2000 se le concedió a Microsoft una patente para filtros bayesianos de correo basura.

Benjamin West. Portrait of Richard Price, 1784. Óleo sobre lienzo, 87,5 × 185 cm. Price acabó convencido de que el teorema ayudaría a probar la existencia de Dios como causa. Después de dos años editando el teorema de Bayes, lo publicó en una revista inglesa. / Llyfrgell Genedlaethol Cymru, The National Library of Wales

La Ilustración

Pero para entender por qué una teoría tan útil había causado tanto revuelo durante la mayor parte del siglo XX, tenemos que remontarnos al comienzo, en tiempos de los reverendos Thomas Bayes y Richard Price, durante los años cuarenta del siglo XVIII. Se había abierto una dura polémica en torno a la improbabilidad de los milagros cristianos. La cuestión era si existían pruebas en el mundo natural que nos ayudaran a alcanzar conclusiones racionales sobre Dios creador, lo que en el siglo XVIII se conocía como la causa o la primera causa.

No sabemos si Bayes intentaba demostrar la existencia de Dios como causa. Pero sí sabemos que trató de enfrentarse matemáticamente al problema de causa y efecto. Sin embargo, Bayes no confiaba lo suficiente en su teorema como para publicarlo. Lo archivó en un cuaderno y no se descubrió hasta que falleció, diez o quince años después. En su testamento, le dejó a Price 100 libras y una petición: que por favor echara un vistazo a sus textos no publicados.

Revisándolos, Price acabó convencido de que el teorema ayudaría a probar la existencia de Dios como causa. Tras dos años editando el teorema de Bayes, lo publicó en una revista inglesa que, por desgracia, leían muy pocos matemáticos.

Unos años más tarde, en 1774, un gran matemático francés, Pierre Simon Laplace, descubrió la regla independientemente de Bayes y Price. Laplace la llamó probabilidad de las causas. A diferencia de Bayes y Price, Laplace era la quintaesencia del científico profesional. Matematizó toda ciencia conocida en su época y pasó cuarenta años desarrollando ocasionalmente lo que conocemos como la regla de Bayes (Laplace, 1812). De hecho, hasta hace unos cincuenta años, la regla de Bayes se consideraba parte de la obra de Laplace. Por derecho, aún deberíamos conocerla como la regla de Laplace.

Tras la muerte de Laplace en 1827, una actitud muy diferente sobre la evaluación de la evidencia científica se apoderó del mundo de la estadística. En el transcurso de los siglos XVIII y XIX en Occidente, los científicos, gobernantes, industriales y clubes de aficionados acumularon una gran cantidad de datos precisos y fiables. Algunas de esas famosas colecciones de datos medían el tamaño del tórax de los soldados escoceses, el número de oficiales prusianos que morían a causa de la coz de un caballo y la incidencia del cólera.

La reacción anti-Bayes

Con una gran cantidad de números precisos y fiables a su alcance, los estadísticos rechazaron la regla de Bayes y prefirieron juzgar la probabilidad de un evento de acuerdo a la frecuencia con la que se producía. Con el tiempo, se les conoció como frecuentistas. Hasta hace unos años, habían sido el gran adversario de la regla de Bayes.

Para los frecuentistas, la ciencia moderna requería tanto objetividad como respuestas precisas. Medir la creencia inicial y subjetiva de alguien y computar las probabilidades y aproximaciones parecía «subjetividad sin control», «una aberración del intelecto» e «ignorancia […] disfrazada de ciencia». Hacia 1920 la mayoría de científicos pensaban que Bayes era «una bofetada de astrología, de alquimia». Y un estadístico importante dijo que la fórmula de Bayes se usaba «con un suspiro de resignación, sabiendo que es el único instrumento que tenemos a nuestro alcance en algunas circunstancias».

«Bayes no confiaba lo suficiente en su teorema como para publicarlo.
Lo archivó en un cuaderno y no se publicó hasta que falleció años después»

Lo sorprendente es que todo este tiempo –mientras teóricos y filósofos denunciaban la aberración subjetivista que según ellos era la regla de Bayes– la gente que tenía que enfrentarse a las urgencias de la vida real y tomar decisiones cruciales basándose en información incompleta seguían utilizando la regla de Bayes. En su opinión, la regla les ayudaba a arreglárselas con lo que tenían.

Así, por ejemplo, la regla de Bayes ayudó a liberar a Dreyfus de una cárcel francesa donde lo había confinado una acusación por traición en la década de 1890. Los oficiales de artillería en Francia, Rusia y los EE UU la utilizaron para apuntar y poner a prueba sus municiones y cañones durante las dos guerras mundiales. Los ejecutivos de las compañías de seguros y las telefónicas también utilizaban la regla de Bayes en los Estados Unidos durante la Primera Guerra Mundial.

Ahora bien, toda buena historia necesita un villano, y el villano de la nuestra es un gran estadístico, Ronald Aylmer Fisher, de la Universidad de Cambridge. Durante los años veinte y trenta del siglo XX, la mecánica cuántica desató una reacción cultural contra la probabilidad y la incertidumbre, y los teóricos estadísticos como Fisher cambiaron su actitud con respecto a Bayes, de tibia tolerancia a absoluta hostilidad.

Jean-Baptiste Guérin Paulin. Pierre-Simon marquis de Laplace (1745-1827), 1838. Óleo sobre tabla, 113 × 146 cm. En 1774 el matemático francés, Pierre Simon Laplace descubrió la regla independientemente de Bayes y Price. Laplace la llamó probabilidad de las causas. / Grand Palais (Château de Versailles)

Los ataques de Fisher fueron especialmente importantes porque era un gigante de una estadística que estaba todavía en pañales (Fisher, 1925). También tenía un temperamento explosivo, que él mismo reconocía que le «amargaba la existencia». Un colega llamó a Fisher «hombre polémico y controvertido. Su vida fue una interminable cadena de altercados científicos –que en ocasiones llegaban incluso a simultanearse–, ya fuera en las reuniones de la profesión o en los artículos propios del oficio». Incluso interpretaba cuestiones científicas como ataques personales. Y odiaba la regla de Bayes.

Fisher no necesitaba a Bayes. Bayes es especialmente útil cuando los datos son escasos e inciertos, y Fisher tenía datos precisos sobre cuánto fertilizante se había utilizado en unos campos determinados. Llenó su casa de gatos, perros y miles de ratones para experimentos de cría y, como buen apasionado de la eugenesia y la genética, documentó el pedigrí de cada animal durante generaciones. Sus experimentos eran repetibles y produjeron respuestas precisas. Calificó la regla de Bayes de «única equivocación (tal vez la única equivocación con el que el mundo de la matemática se haya implicado jamás a fondo) […] fundada en un error y [la regla] ha de ser rechazada por entero». Después de que otro científico y estadístico de Cambridge, Harold Jeffreys, usara la regla de Bayes para encontrar terremotos a partir de los tsunamis que provocaron, Fisher dijo que en su libro sobre probabilidad (Jeffreys, 1931), había cometido «en la primera página de su escrito un error lógico que viene a invalidar las 395 fórmulas del resto del libro». El error, por supuesto, era que utilizaba la regla de Bayes (Aldrich, 2004, 2008).

La Segunda Guerra Mundial

Así pues, al comienzo de la Segunda Guerra Mundial en 1939, Bayes era casi un tabú entre los estadísticos más sofisticados. Afortunadamente para Gran Bretaña y los Estados Unidos, Alan Turing no era un experto en estadística. Era matemático. Dado que necesitaba tomar decisiones urgentes basadas en pruebas exiguas, Turing usó la regla de Bayes ampliamente para, primero, descifrar las órdenes para los submarinos en el Atlántico Norte escondidas en el código Enigma de los alemanes; y segundo, para construir las computadoras Colossus, diseñadas para descifrar otros códigos alemanes durante la guerra.

«Gracias a Bayes podemos filtrar correo basura, evaluar riesgos médicos, buscar las páginas que nos interesan en Internet y descubrir lo que quizás nos interesaría comprar»

Después de la Pax Europaea, sin embargo, el gobierno británico clasificó como secreto de estado todo aquello que mostrara que las matemáticas, la estadística, las decodificaciones, las computadoras y Alan Turing habían ayudado a ganar la guerra. Quién sabe si el decreto impidió que el Reino Unido se convirtiera en líder de la revolución informática del siglo XX. Desde luego impidió que matemáticos y estadísticos se convirtieran en héroes de guerra.

Dado que sus éxitos bélicos quedaron clasificados, la regla de Bayes llegó al final de la Segunda Guerra Mundial despertando más suspicacias que antes. Después de que Jack Good, el asistente estadístico de Turing durante la guerra, expusiera los detalles del método ante los miembros de la Real Sociedad Estadística británica, las primeras palabras del siguiente orador fueron: «Tras estas estupideces…» Los profesores de la Escuela de Estudios Empresariales de Harvard decían que sus colegas bayesianos eran unos «socialistas que se autodenominaban científicos». Cuando Hans Buehlmann, futuro presidente de la Escuela Politécnica Federal de Zúrich (ETH), visitó el departamento de estadística de Berkeley, profundamente frecuentista, afirmó que «era poco menos que peligroso exponer el punto de vista bayesiano». Así que utilizó el método de Bayes pero inventó una terminología diferente y neutral que, en su opinión, protegía a la Europa continental de gran parte del desprecio angloamericano.

Durante la Guerra Fría, la Fuerza Aérea de los Estados Unidos perdió una bomba de hidrógeno en la costa de Palomares, y la Marina de los Estados Unidos comenzó a desarrollar la teoría bayesiana en secreto para encontrar objetos bajo el agua. En la imagen, el casquillo de dos bombas nucleares B28 del incidente de Palomares, expuestas en el Museo Nacional de la Ciencia y la Historia Nuclear, en Albuquerque, Nuevo México. / Plumbob78

Irónicamente, cuando Bayes se convirtió en un tema tabú, el ejército estadounidense continuó utilizándolo en secreto. Por ejemplo, un estudio clasificado de la Corporación RAND en California usó la regla de Bayes para avisar a la Fuerza Aérea de los Estados Unidos de que continuar pilotando aviones armados con bombas de hidrógeno por el mundo podía causar más accidentes como el de Palomares. La administración Kennedy finalmente añadió dispositivos de seguridad. La Marina de los Estados Unidos la utilizó para encontrar submarinos soviéticos en el Mediterráneo. En 1973, el primer estudio de seguridad de la industria de energía nuclear de Estados Unidos se basó en métodos bayesianos y predijo lo que pasaría durante el accidente de 1979 en Three Mile Island, Pennsylvania.

Resurgimiento y prueba de su valor

Sin conocer los éxitos de la regla de Bayes, un pequeño grupo de poco más de cien creyentes pelearon por reivindicarlo durante la Guerra Fría. Muchos bayesianos de esa generación recuerdan el momento exacto en que la lógica general de Bayes les alcanzó de repente como una epifanía. Para ellos, la regla de Bayes tenía lo que Einstein llamó «el sentimiento religioso del cosmos».

La batalla entre estadísticos bayesianos y antibayesianos se volvió tan corrosiva y personal que, en una fiesta a mediados de los sesenta a la que un bayesiano estadounidense llevó a su hijo de nueve años, un invitado le dijo al chico que «su padre era un hombre profundamente engañado».

Izquierda: El ejército estadounidense usa la regla de Bayes para mejorar las imágenes generadas durante el vuelo de los drones. / Don McCullough. Derecha: El coche sin conductor de Google comienza a rodar con la información de mapas de ruta y de las condiciones de la carretera. A medida que el automóvil se mueve en entornos de tráfico, los sensores que lleva encima recogen nuevos datos de tráfico para actualizar la información inicial y calcular cuál es probablemente la conducción más segura en ese momento. / Steve Jurvetson

Durante este período angustioso, José M. Bernardo, un profesor de estadística de la Universitat de València, utilizó métodos bayesianos radicalmente novedosos en aquel momento para realizar análisis políticos. Realizó un análisis bayesiano de encuestas políticas para el Partido Socialista en 1982, durante la campaña electoral que le daría el poder a Felipe González. La regla de Bayes es útil para actualizar hipótesis con datos muy diversos, incluyendo la probabilidad de actitudes y tendencias de voto. Más tarde, Bernardo se convirtió en asesor científico del gobierno durante la presidencia de González y llevó a cabo otras aplicaciones bayesianas. Al mismo tiempo, Bernardo también había representado un papel importante para fomentar una cierta camaradería bayesiana. Convenció al primer gobierno democrático (centrista) tras la dictadura fascista de que financiar un congreso internacional para estadísticos bayesianos en 1979 ayudaría a publicitar el emergente estado democrático español. El esfuerzo tuvo tanto éxito que el gobierno valenciano financió una segunda y una tercera conferencia. Después de eso, no se necesitaban subvenciones, ya que se consideraba un privilegio ser invitado a la conferencia y los estadísticos podían obtener dinero fácilmente de sus instituciones para el viaje. Otros fondos proporcionaron becas a nuevos doctorados. Las reuniones, que se celebraban cada cuatro años, eran vitales para que los bayesianos desarrollaran un sentimiento de solidaridad, para reavivar los espíritus y discutir los últimos métodos y teorías. Con los años, las conferencias crecieron de alrededor de cien asistentes a tantos que tuvieron que trasladarse a instalaciones cada vez más grandes. Ahora una organización interna­cional de bayesianos (ISBA) continúa organizándolos cada dos años: en Kyoto, Japón, en 2012 y en Cancún, México, en 2014.

Durante la década de 1990 el panorama cambió radicalmente para la regla de Bayes. Potentes ordenadores de sobremesa, nuevos métodos computacionales y el software libre finalmente permitieron a los bayesianos calcular problemas reales con facilidad. Estudiosos de la informática, la física y la inteligencia artificial llegaron en masa revitalizando, ampliando, despolitizando y secularizando el mundo de la estadística. Después de 250 años de vaivenes, la teoría se adoptó de un día para otro.

Alan Turing usó la regla de Bayes ampliamente para, primero, descifrar las órdenes para los submarinos en el Atlántico Norte escondidas en el código Enigma de los alemanes; y segundo, para construir las computadoras Colossus, diseñadas para descifrar otros códigos alemanes durante la guerra. En la imagen, una estatua del matemático en el Bletchley Park Museum. / Duane Wessels (Bletchley Park Museum)

Durante los últimos años, Bayes se ha convertido en una figura que muchos estadounidenses modernos piensan que hay que conocer. Por ejemplo, cuando Alan B. Krueger se convirtió en miembro del consejo de asesores económicos del presidente Obama, realizó una mención completamente gratuita de mi libro sobre Bayes (McGrayne, 2013) en el New York Times: «Recientemente he terminado de leer el libro de McGrayne […] la regla de Bayes es una teoría estadística con una historia larga e interesante. Es importante en la toma de decisiones –lo estricto que hay que ser aferrándose a ideas propias y cómo hay que actualizar esas ideas a medida que se va recibiendo nueva información. Nosotros […] [y recordemos que es consejero de Obama] usamos la regla de Bayes intuitivamente cada día.»

Así que de repente en esta era dogmática, cuando muchos líderes están orgullosos de tomar decisiones basadas en la doctrina que recibieron de niños, Bayes se ha convertido en la clave política para algo diferente: la toma de decisiones basadas en datos. Tras un notable desarrollo, la estadística bayesiana –que fue campo de estudio de clérigos y de cien creyentes acosados durante la Guerra Fría– es ahora parte del vocabulario de la Casa Blanca.

La revolución bayesiana ha resultado ser un cambio de paradigma moderno para una era eminentemente pragmática. Sucedió de la noche a la mañana. No porque la gente cambiara de opinión sobre la regla de Bayes como filosofía científica, sino porque de repente la regla funcionaba.