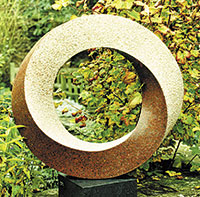|
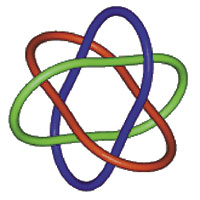
John Robinson’s Symbolic Sculpture. J. Robinson’s symbolic sculpture is inspired by a diversity of mathematical motifs. The author looks at two of these in particular: the fibre bundles and Borromeo’s rings, which reflect the artist’s outstanding mathematical intuition. Aunque la asociación de matemáticas y arte puede parecer en principio extraña, ambas materias comparten su interés común por las estructuras y las formas. Para los investigadores, las matemáticas son una aventura en el mundo de las formas, donde los cálculos y el rigor son las herramientas utilizadas. A los matemáticos nos gusta, fundamentalmente, investigar la lógica de la forma y sus relaciones con otras formas, calcular, entender, describir, descubrir las complejidades y la belleza de una situación. Nos gusta conocer lo que es cierto, no sólo en un caso particular sino también en general. Matemáticas y arte tienen objetivos diferentes pero algunos fundamentos comunes. El arte pretende conseguir algunos “puntos de agarre” sobre las emociones, y para ello se apoya en el concepto de estructura y en un elemento estético de proporción y ritmo. En las matemáticas, el elemento estético también representa un papel importante para determinar qué áreas, resultados o modos de demostración son considerados interesantes e incluso bellos. Creation. Es un placer hacer esta introducción a las matemáticas relacionadas con un artista moderno que está fascinado con las estructuras geométricas y por las teorías científicas sobre nuestro sitio en el universo y que es capaz de expresarlo en su arte. En 1989, cuando conocí a John Robinson, quedé muy sorprendido con su formación. Aburrido del tipo de vida que llevaba en una escuela privada inglesa, a pesar de haber ganado algunos premios en geometría y escultura, a los dieciséis años decidió enrolarse en la marina mercante inglesa. Desembarcó en Australia, donde vivían algunos familiares lejanos. Pasó unos años pastoreando rebaños o trabajando en la patrulla de la policía rural de los Kimberlies antes de asentarse durante diez años en el desierto de Ninety Miles, donde puso en marcha una explotación de corderos. Se casó y empezó su vida familiar. Hacia el final de estos diez años, cuando la explotación ya funcionaba casi sola, compró arcilla y empezó a modelar a sus hijos y amigos. A los 35 años, cansado del terrible calor y de las moscas del verano australiano en el desierto, decidió vender su explotación y con el dinero obtenido vivir dos años, él y su familia, en Inglaterra, donde aún vivía su madre. Allí siguió modelando figuras de niños jugando o descansando, amantes, madre e hijo, jóvenes realizando algún tipo de deporte… Empezó a vender sus esculturas y decidió quedarse en Inglaterra. Alrededor de 1975 empezó a trabajar en las esculturas simbólicas, así nació la serie Univers. El concepto “símbolo” es la clave de esta serie, ilustrada por el contraste entre la escultura figurativa Acrobats y la escultura simbólica Elation (Gozo). Las formas que él expresa en la serie Univers nacen de su vida y su experiencia, pero se ve forzado a buscar símbolos dentro de la geometría: esferas, ovoides, conos, cuadrados, pirámides… Los títulos de sus esculturas simbólicas no pretenden ser descriptivos sino una “puerta” y una indicación de que la forma no es una abstracción sino un símbolo. Bonds of Friendship. Desde 1990, copias de diversas esculturas de la serie Univers han sido exhibidas en distintas universidades, como por ejemplo, la de Oxford, Cambridge, Gales, Liverpool, Leeds, Barcelona, Zaragoza,… Robinson es un geómetra experimental notable, como puede verse al estudiar sus esculturas simbólicas. De entre los diversos motivos matemáticos que han inspirado las esculturas simbólicas de Robinson he seleccionado dos: los fibrados y los anillos de Borromeo. Fibrados El modelo más fácil de cinta de Moebius es tomar una tira larga de papel y pegar los extremos después de realizar un giro de 180 grados. Es un modelo de una superficie de una sola cara y con borde conexo. Podemos ver la cinta de Moebius de otra manera. La cinta contiene una circunferencia en el centro y podemos pensar que está formada por segmentos iguales que cortan dicha circunferencia en ángulos rectos. Así, la podemos ver como un segmento que va girando a medida que lo trasladamos a lo largo de dicha circunferencia. Muchos artistas han quedado fascinados con las superficies de una sola cara, en especial con la cinta de Moebius. John Robinson fue uno de ellos y se dió cuenta de que, si en lugar de un segmento, trasladamos otras formas geométricas a lo largo de una circunferencia y con diferentes ángulos de giro, ello proporciona figuras diferentes, siempre dependiendo de la forma geométrica con la que empecemos y del ángulo de giro elegido. De esta manera, Robinson descubrió un concepto muy importante en matemáticas: los fibrados. Un fibrado es un objeto matemático que consiste en un espacio base, que para la cinta de Moebius y otras esculturas de Robinson es la circunferencia. La fibra es la figura que se traslada a lo largo de la circunferencia. Una información extra que sirve para definir el objeto o espacio total del fibrado es el ángulo de giro de la fibra cuando se traslada a lo largo de la circunferencia. Dicho ángulo tiene que estar relacionado con la forma de la fibra para que las fibras “se enganchen bien” y den el espacio total del fibrado. Cuando la fibra es un segmento, los ángulos posibles son los múltiplos de 180º. En particular, si tomamos un ángulo de giro nulo obtenemos la superficie de un cilindro que tiene dos caras y un borde formado por dos circunferencias. Para el caso de la cinta de Moebius, la fibra es también un segmento pero el ángulo de giro es de 180º; ahora obtenemos una superficie con sólo una cara y que tiene por borde una curva cerrada simple. Si tomamos como fibra un triángulo equilátero, el ángulo de giro tendría que ser cualquier múltiplo de 120º. El caso más sencillo de nuevo, correspondiente al giro de 0º, daría simplemente una rosquilla de sección triangular. Los vértices describen tres circunferencias que no se cortan. La escultura Eternity se hizo usando un giro de 120º y en este caso, si seguimos el recorrido de cualquiera de los vértices, tendremos una curva que sólo se cierra al cabo de tres vueltas y nos da un nudo de trébol. En las fotografías se pueden observar algunos de los pasos seguidos para su construcción donde se muestra, claramente, la fibra triangular del fibrado. Usando un giro de 120º también se ha construido Gordian Knot (Nudo gordiano); en este caso la fibra es la unión de tres círculos tangentes entre sí, como se ve en la figura 1. En el caso de que usemos como fibra un cuadrado, el ángulo de giro tiene que ser un múltiplo de 90º. La escultura Dependent Beings (Seres dependientes) está hecha con un giro de 180º. Pienso que lo que Robinson ha conseguido es mostrar que estas formas, que pueden describirse con términos matemáticos, también pueden transformarse en objetos de una sorprendente belleza con una adecuada elección del material y de las proporciones. El concepto de fibrado es tan general que describe nuevas clases de objetos que son difíciles de visualizar ya que sólo es posible realizarlos propiamente en un espacio de muchas dimensiones. Supongamos, por ejemplo, que cambiamos el espacio base de la cinta de Moebius por un objeto algo más complejo como puede ser una esfera. La fibra podría ser uno de los cinco sólidos platónicos (tetraedro, cubo, octaedro, dodecaedro o icosaedro). ¿Cómo podríamos describir y entender la geometría, las relaciones espaciales, de los objetos resultantes? ¿Cuántos objetos de este tipo hay? Preguntas como estas son las que intentan responder las matemáticas. Los anillos de Borromeo Como se puede observar en la figura 2, los anillos de Borromeo son tres circunferencias engarzadas entre sí de modo que ninguna puede separarse de las otras, pero manteniendo cada una su independencia. Esto es un ejemplo de lo que los matemáticos llamamos un engarce de tres componentes conexos. El estudio de este tipo de engarces forma parte de la teoría de nudos. El nombre proviene de una familia italiana, los Borromeo, que empezaron a usarlo en el emblema familiar en el siglo XV, si bien es cierto que se han encontrado motivos relacionados con estos anillos en la cultura celta y vikinga. Si uno intenta construir los anillos de Borromeo con hilo de alambre se da cuenta de que es imposible hacerlo usando circunferencias planas, siempre tiene que doblarlas un poco (figura 3). En la literatura existen varias demostraciones rigurosas de la imposibilidad de construir los anillos de Borromeo usando circunferencias planas. Por ejemplo, una elemental es la de B. Lindström y H. O. Zetterström (1991)¹. Sin embargo, sí que es posible construirlos usando elipses en lugar de circunferencias (figura 4). John Robinson, experimentando con cuadrados, se dio cuenta de que usando cuadrados en lugar de circunferencias es posible construir los anillos de Borromeo. De este modo creó su escultura Creation y fue sorprendente la figura de enorme belleza que consiguió. Uno puede entretenerse en construir por sí mismo en cartulina unos anillos de Borromeo con forma de cuadrado y comprobar que si elige bien la longitud del lado, la estructura se puede plegar; tendríamos así una escultura transportable. Unos cinco años después de haber hecho Creation visitó el mausoleo de Ismail Samanid de Bujara (Uzbekistán). Se trata de un pequeño edificio considerado la perla de la arquitectura islámica, pero que en realidad fue construido en el año 907 –poco antes de la islamización de la zona– por los seguidores del zoroastrismo como templo para la adoración del fuego. Encima de cada una de las cuatro entradas al templo hay grabados en piedra dos símbolos, uno de ellos es el cuadrado dentro del cuadrado dentro del cuadrado, imaginaos su sorpresa cuando la guía comentó que era el símbolo de la creación para los seguidores del zoroastrismo. Intuition está construida aprovechando la idea de los anillos de Borromeo pero con triángulos en lugar de cuadrados. Para Robinson representa el núcleo anudado de la estabilidad en el centro del conocimiento personal. De él salen, a menudo sin razón aparente, destellos de originalidad y de descubrimiento. Estos destellos, que llamamos intuición, aparecen en todas direcciones pero provienen del núcleo de la experiencia. Muchos lectores habrán visto la película 2001 Una odisea del espacio y sin duda recordarán las escenas iniciales: la intuición representa un papel importante en el progreso de las especies. Intuition. Un cierto tiempo después de finalizar esta escultura, recibió una carta de Peter Cromwell en la que incluía una fotografía de la Piedra de las Leyendas, una pieza escandinava del siglo IX que mostraba la estrella de Wotan y que resulta que es una versión de la escultura Intuition. Se podría decir que la intuición de Isaac Newton cambió el mundo, por lo que Robinson considera que es un honor increíble que su escultura Intuition esté en la entrada del Institute Isaac Newton de Cambridge. También considera un gran honor que una reproducción fuera donada en 1997 al Fields Institute for Research in Mathematical Sciences de Toronto con motivo del 90 cumpleaños del matemático H.S.M. Coxeter. Otra construcción de gran belleza se consigue también utilizando rombos. En este caso Robinson la tituló Genesis. En la serie Univers de Robinson hay otras esculturas, aparte de Creation e Intuition, mencionadas anteriormente, que son ejemplos de nudos o engarces estudiados en la teoría de nudos, como por ejemplo: Bonds of Friendship, que es un engarce de Hopf; Rhythm of Life, que contiene un nudo toroidal (15, 4), esto es, que da quince vueltas alrededor del cuerpo de la rosquilla y cuatro alrededor del hueco central; y, finalmente Immortality, un nudo llamado de trébol, que, con la notación anterior, se expresaría como un nudo (2, 3). Notas Las fotografías de las esculturas se reproducen por cortesía de J. Robinson y Edition Limitee. |
Acrobats. Elation. Eternity es una escultura en bronce de 1,5 metros de altura realizada por J. Robinson en 1980. En las tres fotografías de debajo aparece el escultor (a la derecha, en la primera fotografía) realizando un modelo en madera. Para hacerlo preparó cien triángulos equiláteros perforados por el centro y los insertó en un aro haciéndolos girar poco a poco, de manera que al final del recorrido cada vértice coincidiera con el contiguo. Así se consigue que los vértices formen una sola curva cerrada y los lados del triángulo den origen a una única banda que recubre toda la superficie y que para el autor simboliza la eternidad.
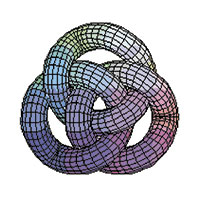
Gordian Knot. Escultura en bronce de 1 metro de altura realizada en 1982. Se basa en la misma idea que la anterior, pero se ha sustituido el triángulo por tres círculos, de manera que se obtiene un nudo triple.
Dependent Beings. En esta escultura, la figra que se hace girar alrededor de una anilla es un cuadrado, de manera que sus lados originen una superficie de dos caras. El artista ha aplicado acabados de textura diferente en cada una para simbolizar la masculinidad y la feminidad, que se unen para convertirse en un ser único. Figura 2.
«Experimentando con cuadrados, se dió cuenta de que usando cuadrados en lugar de circunferencias es posible construir los Anillos de Borromeo»
Genesis. Rhythm of Life.
Immortality.
Figura 3.
Figura 4. |