El bañista de Siracusa

Ilustración: Hugo Salais

De pequeña, mi referente de sabio loco con pelo blanco era Arquímedes. Mi libro de cabecera entonces, el Dime quién es, contaba la historia de su loca carrera, desnudo, gritando «¡Eureka!» por toda Siracusa, tras dar con la solución al problema que le obsesionaba: si la corona del rey Hierón era de oro o el orfebre le había engañado dorando otro metal. Quizá por decoro de libro infantil, la ilustración lo mostraba poco antes, en la bañera, mirando el aumento del nivel del agua tras entrar en ella. Yo también empecé a fijarme cuando me bañaba, sin llegar al momento «¡Equilicuá!», como habría dicho mi abuela Severiana. Cuando, de mayor, estudié hidrostática, lo del nivel del agua en la bañera no me pareció una observación especialmente genial. ¿Qué descubrió Arquímedes realmente? Y, ¿con qué propósito?

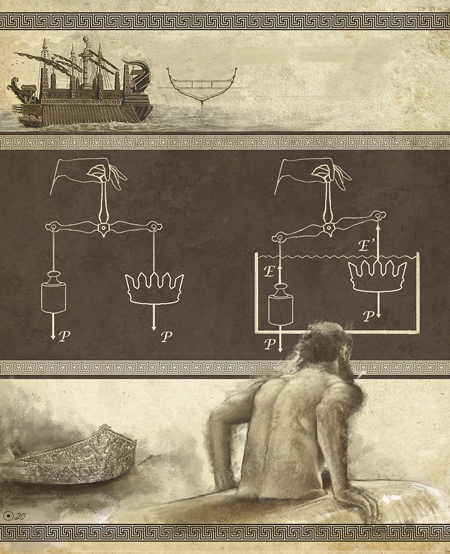
Si sostenemos un objeto sobre la mano, sentimos su fuerza de contacto (igual al peso del objeto). Ahora sumergimos mano y objeto (este no debe flotar) bajo el agua y notamos que la fuerza de contacto disminuye. Se debe a que aparece el empuje E, que solo depende de la masa de agua desplazada por el objeto al sumergirlo en ella y es debido al hecho de que la presión del agua aumenta con la profundidad. Sobre dos bolas iguales, una de plomo y otra de corcho, introducidas totalmente en agua, se tiene el mismo empuje. El peso de la bola de corcho es menor que E, luego, al soltarla, sube y flota (y deja una parte fuera del agua). El peso de la de plomo es mayor que E y la bola se hunde. Si transformo la bola de plomo en un vaso o cuenco hueco, el peso no cambia, pero ahora el empuje es mayor: desplaza más masa de agua y consigo que flote. Por otro lado, y como ilustra la figura en la página anterior, dos cuerpos pueden tener el mismo peso P y al introducirlos en un fluido, la balanza se desequilibra: significa que sus volúmenes son diferentes (diferentes empujes E y E’) y están hechos de diferentes materiales.

«El historiador de la ciencia Alexander Koyrè resumió el trabajo científico del siglo XVI como una comprensión gradual de las obras de Arquímedes»

Se sabe que Arquímedes, al igual que otros científicos helenísticos, abordó muchos problemas físicos y matemáticos, y numerosos proyectos tecnológicos, como la manus ferrea (garra) que destruyó la armada romana, el architronito –cañón a vapor recuperado por Leonardo da Vinci–, o el diseño de engranajes y poleas, como los que usó para botar el Siracusia, una especie de Titanic de lujo con una carena tan grande, para aumentar el empuje, que no podía fondear en casi ningún puerto. También supervisó su construcción y diseñó las catapultas defensivas de cubierta contra el pirateo.

Galileo Galilei despotricaba contra Vitruvio (origen de la leyenda del «eureka») por banalizar la sofisticación científica del siracusano. De hecho, el historiador de la ciencia Alexander Koyrè resumió el trabajo científico del siglo XVI como una comprensión gradual de las obras de Arquímedes. Entre ellas, el tratado «sobre los cuerpos flotantes» que analiza la estabilidad de cuerpos que tienen forma de cuenco o paraboloide: la forma de cualquier nave. Basándose en él, Galileo reconstruyó el método para determinar la densidad de un cuerpo, usado también hoy día. Le habría gustado el Arquímedes pintado por su coetáneo José de Ribera: de tez mediterránea, enjuto y calvo, con mente absorta y sonrisa maliciosa, pensando «¡Equilicuá!».