Ilustración: Raquel Garcia Ulldemolins
Si Euclides, el padre de la geometría, hubiese conocido Manhattan, posiblemente le habría hecho dudar sobre aquello que decimos constantemente de que «la distancia más corta entre dos puntos siempre es la línea recta». Ya sea en la Gran Manzana o en cualquier otra ciudad, si para diseñar una ruta en una zona donde haya edificios usamos la línea recta para unir el origen y el destino de la misma, nos encontraremos con el pequeño inconveniente de que nuestra ruta debe atravesar algún inmueble.
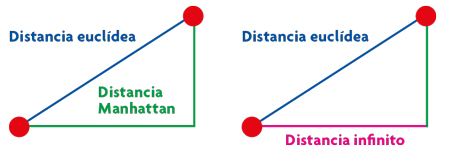
En la geometría que nos enseñó el gran matemático griego –que es la que aprendemos en los primeros años de la escuela– la distancia entre dos puntos se mide como la longitud del segmento que los une. Esta forma de medir la distancia es conocida como «distancia euclídea» y tiene infinidad de aplicaciones en matemáticas y en nuestra vida cotidiana. Sin embargo, no es la única forma de hacerlo y no siempre es real en según qué problemas queramos resolver: por ejemplo, el de la ruta mínima en medio de una ciudad. Si los puntos que debemos conectar con el camino más corto están cada uno de ellos en un lateral de una manzana de edificios, el camino más corto entre ellos vendrá dado por la suma de los dos catetos de un triángulo rectángulo.
Es a esta suma de longitudes a lo que llamamos «distancia Manhattan» (o más formalmente, distancia L1). Es mayor que la distancia euclídea pero también es más real en la práctica. De hecho, la distancia Manhattan entre dos puntos se calcula como la longitud de cualquier camino que los una mediante segmentos verticales y horizontales; todos miden lo mismo.
Cuando se trata de diseñar rutas de recorrido mínimo en ciudades, tiene más sentido usar esta distancia que la euclídea; por no ir atravesando rascacielos, por ejemplo. Es más, puesto que todas las «escaleras» tienen la misma longitud, nos permite elegir entre distintas opciones, en función de semáforos, zonas de dudosa seguridad, manifestaciones, etc.
Evidentemente, no todas las ciudades, ni siquiera Nueva York, están distribuidas como una cuadrícula, pero se suele considerar para muchos tipos de problemas de diseños de rutas este tipo de distancia. Y también, cómo no, en el diseño de circuitos ortogonales en los que predominan las conexiones en vertical y horizontal, o en el de un plano de metro.
Existen muchas distancias además de la euclídea y la Manhattan. Otra muy conocida es la «distancia infinito» (más formalmente, distancia de Chebyshev). La distancia infinito mide la longitud del cateto más largo del triángulo rectángulo que definen dos puntos. Dicho más formalmente, la mayor diferencia entre sus coordenadas. Posiblemente, el uso más conocido de esta otra forma de medir las distancias se encuentra en los movimientos del rey del ajedrez, ya que coincide con el número mínimo de movimientos que necesita el rey para ir de una casilla a otra.
«La distancia Manhattan es mayor que la distancia euclídea, pero también es más real en la práctica»
Otro de los aspectos llamativos tanto de la distancia Manhattan como de la distancia infinito es que las circunferencias con estas no son redondas. Como lo oyen: una circunferencia con centro en un punto P y radio R es la curva que describen los puntos que están a distancia R de P. Pues bien, con la distancia Manhattan tenemos un rombo y con la distancia infinito, un cuadrado. En ambos casos, centrados en P. Por lo tanto, con estas distancias se acabó también la expresión de «x kilómetros a la redonda» y nuestra idea intuitiva de círculo.