Cuando la tecnología va más rápido que la comprensión

El aprendizaje profundo es un tema indiscutiblemente candente, no solo entre académicos e industria, sino también en la sociedad y en los medios de comunicación. Las razones de este crecimiento de popularidad son múltiples: una disponibilidad sin precedentes de datos y potencia de cálculo, la aparición de algunas metodologías innovadoras, trucos técnicos menores pero significativos, etc. Sin embargo, resulta curioso que el éxito actual y la práctica del aprendizaje profundo parecen no estar correlacionados con su comprensión más teórica y formal. Debido a esto, la vanguardia tecnológica del aprendizaje profundo presenta una serie de propiedades o situaciones poco intuitivas. En este texto se resaltan algunas de estas propiedades poco intuitivas, tratando de mostrar trabajos recientes relevantes y de evidenciar la necesidad de saber más sobre ellos, ya sea mediante métodos empíricos o formales.

Palabras clave: aprendizaje profundo, aprendizaje automático, redes neuronales, propiedades poco intuitivas.

Introducción

En los últimos años, las redes neuronales han resurgido de sus cenizas y han producido resultados impresionantes en tareas para las cuales el rendimiento de los métodos tradicionales era sistemáticamente inferior (LeCun, Bengio y Hinton, 2015). Las razones de este éxito son muchas, y siguen siendo tema de debate. Claramente, la contribución de ciertos datos y componentes tecnológicos, como la disponibilidad de volúmenes de datos sin precedentes y el acceso generalizado a una mayor potencia de cálculo, ha sido decisiva. Sin embargo, además de estos componentes más prácticos, podríamos decir con seguridad que uno de los principales facilitadores del éxito actual de las redes neuronales ha sido la introducción de algunos «trucos del oficio» menores pero significativos. Algunos ejemplos fueron la inicialización de los pesos de las neuronas mediante entrenamiento previo no supervisado, la sustitución de las activaciones sigmoideas por unidades lineales rectificadas para aliviar el problema de la desaparición de los gradientes, o el uso sistemático y amplio de arquitecturas convolucionales para abordar las traducciones reduciendo el número de pesos entrenables.

«En los últimos años, las redes neuronales han resurgido de sus cenizas y han producido resultados impresionantes»

Curiosamente, la mayoría de estos trucos útiles no surgen de una teoría unificada de redes neuronales ni de desarrollos matemáticos rigurosos. Por el contrario, surgen de la intuición, de la investigación empírica y, en última instancia, del ensayo y error (o de búsquedas por fuerza bruta). En este sentido, la investigación en aprendizaje profundo parece seguir el paradigma de Wolfram de «un nuevo tipo de ciencia», que indica que «solo podemos acercarnos al diseño óptimo de los sistemas [de aprendizaje profundo] mediante una búsqueda combinatoria entre la ingente cantidad de configuraciones posibles [de la red]» (Wolfram, 2002). De hecho, algunos investigadores han abrazado este mantra directamente y han comenzado a buscar guiados parcialmente por metodologías automáticas o estructuradas. Por ejemplo, Zoph y Le (2016) descubren nuevas configuraciones de red utilizando estrategias evolutivas.

Pero el avance empírico de la disciplina no debería evitar el desarrollo de teorías más formales (o prototeorías) que nos permitan entender qué está ocurriendo y, con el tiempo, proporcionen una comprensión más holística de este campo de investigación. En particular, esta comprensión podría llegar gracias a una serie de cuestiones abiertas o propiedades poco intuitivas de las redes neuronales que desconciertan a la comunidad de investigadores (Larochelle, 2017). En el resto del artículo presentaré e intentaré explicar brevemente algunas de estas propiedades.

Les redes neuronales pueden cometer errores absurdos

Ahora es bien sabido que las redes neuronales pueden generar resultados completamente inesperados a partir de entradas con cambios perceptivamente irrelevantes, conocidos habitualmente como ejemplos adversarios. Los humanos también pueden verse desconcertados por «ejemplos engañosos»: todos hemos visto imágenes que identificábamos como algo (o parte de algo) y que después hemos descubierto que eran otra cosa distinta. Sin embargo, la cuestión aquí es que los ejemplos engañosos humanos no se corresponden con los de las redes neuronales porque estos últimos pueden ser perceptivamente iguales. Szegedy et al. (2014) mostraron que una red puede clasificar erróneamente una imagen con solo aplicarle «una cierta perturbación apenas perceptible». No solo eso, también descubrieron que la misma perturbación de esa imagen en particular provocaba el error de clasificación incluso cuando la imagen no estaba en el grupo de entrenamiento; es decir, cuando se había entrenado a la red con un subconjunto de imágenes diferente. De igual forma, Nguyen, Yosinski y Clune (2015) mostraron que es posible producir imágenes artificiales que son completamente irreconocibles para los humanos pero que, no obstante, las redes neuronales profundas pueden relacionar con objetos reales con una confianza del 99,99 %.

El problema de los ejemplos adversarios es interesante porque estos contradicen una de las cualidades más conocidas y extensamente demostradas de las redes neuronales: su gran capacidad de generalización (o, en otras palabras, su rendimiento excepcional con datos nuevos). Cada vez sabemos más sobre potenciales ataques adversarios (Papernot et al., 2017), y con este conocimiento aparecen nuevas técnicas para enfrentarse al problema. Han aparecido teorías incipientes, y el trabajo reciente sugiere que los ejemplos adversarios están directamente relacionados con el rendimiento modelo (Gilmer et al., 2018). Sin embargo, hasta el día de hoy seguimos sin alcanzar una comprensión general del fenómeno.

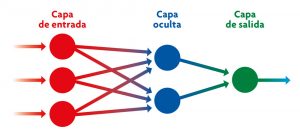
Las redes neuronales artificiales toman como modelo el sistema neuronal de un cerebro biológico. Cada nodo del esquema representa una de estas neuronas situadas a distintos niveles (capa de entrada, oculta y de salida) que procesan los datos con los que se las «entrena» en el proceso de aprendizaje profundo. / Adaptado de Wikipedia

El espacio de soluciones es un misterio

Como con muchos otros algoritmos de aprendizaje automático, el entrenamiento de redes neuronales opera encontrando la combinación de números –llamada parámetros de la red o pesos– que ofrece el mayor rendimiento o, mejor dicho, la menor pérdida de algunos datos. Si tuviéramos un único peso, entrenar a la red consistiría en encontrar el valor de dicho peso que ofrece la menor pérdida de información. Existen metodologías muy conocidas que ofrecen garantías teóricas para encontrar ese mínimo en casos que incluyen una pequeña cantidad de parámetros. Sin embargo, las redes neuronales profundas suelen tener varios millones de parámetros, y hay que combinarlos de manera apropiada para minimizar una determinada pérdida. El número de parámetros no sería de por sí un problema grave si la pérdida fuera convexa; es decir, si tuviera un único mínimo y, grosso modo, todos los caminos descendentes llegaran a dicho mínimo. Pero esto no es así. Las pérdidas de las redes profundas actuales no son convexas y tienen múltiples mínimos locales.

En este escenario, no hay muchas garantías teóricas de la utilidad de la mayoría de metodologías conocidas para encontrar un buen mínimo (idealmente el menor de todos los mínimos). En general, los perfiles de pérdida inducidos por las redes profundas son completamente desconocidos, y se ha explorado solo una minúscula fracción del espacio de soluciones. Además de múltiples mínimos locales, se supone que los perfiles de pérdida incluyen puntos de ensilladura (Dauphin et al., 2014) y otros obstáculos que teóricamente dificultan la «navegación» de los algoritmos actuales de búsqueda de mínimos. No obstante, algoritmos muy sencillos de búsqueda de mínimos extremadamente básicos consiguen buenas soluciones; lo suficientemente buenas como para abordar diferentes problemas de vanguardia bien definidos, y para enfrentarse a tareas de aprendizaje automático nuevas e impensables hasta entonces. ¿Por qué ocurre esto?

«Es interesante que el campo del aprendizaje profundo pueda presentar tantos avances y, a la vez, tantas situaciones desconcertantes»

Una hipótesis común es que la gran mayoría de los mínimos locales tienen pérdidas similares; esto es, todos ellos implican soluciones igualmente buenas (Kawaguchi, 2016). Otra hipótesis es que, utilizando los métodos actuales de búsqueda de mínimos, no se detectan los puntos de ensilladura y otros obstáculos (Goodfellow, Vinyals y Saxe, 2015). También es muy posible que algunas arquitecturas o cuestiones previas del diseño introduzcan la convexidad (Li, Xu, Taylor y Goldstein, 2017). Todo ello podría explicar por qué funcionan realmente las inicializaciones de peso aleatorias, así como los algoritmos de búsqueda de mínimos más simples. De hecho, estos algoritmos parecen funcionar mejor cuando están mal condicionados, o cuando se introduce ruido en el proceso.

Les redes neuronales pueden memorizar con facilidad

Incluso una red neuronal no muy profunda es parte de lo que se conoce como algoritmos universales de aproximación de funciones (Cybenko, 1989). En pocas palabras, esto significa que las redes neuronales son suficientemente potentes para representar cualquier conjunto de datos. La investigación reciente muestra de manera empírica que las redes de tamaño finito pueden modelar cualquier conjunto finito de datos, incluso si está compuesto de datos mezclados, datos aleatorios o etiquetas aleatorias (Zhang, Bengio, Hardt, Recht y Vinyals, 2017). La implicación de esto es que las redes neuronales pueden recordar las etiquetas de cualquier dato del entrenamiento, sin importar la naturaleza de este. Y recordar los datos del entrenamiento implica funcionar con un cien por cien de precisión con esos datos.

Lo que no es tan obvio es que, si los datos no son completamente aleatorios, las redes neuronales son totalmente capaces de extrapolar sus recuerdos a casos nuevos y generalizar. Que logren esto cuando el número de parámetros modelo es varios órdenes de magnitud mayor que el número de instancias de entrenamiento es lo que resulta intrigante y todavía no tiene una justificación formal. Contradice la clásica regla de oro del aprendizaje automático, que prefiere modelos simples (que incluyan pocos parámetros que aprender) para alcanzar buenos resultados en la generalización. También contradice la idea convencional de que hay que utilizar alguna forma más o menos explícita de poda de parámetros irrelevantes, un proceso comúnmente conocido como regularización, cuando el modelo es mucho más grande que el número de instancias de entrenamiento (Zhang et al., 2017).

Las redes neuronales pueden comprimirse

La poda de parámetros o la regularización explícita no es necesaria para generalizar. Sin embargo, se sabe que se puede reducir el número de parámetros de una red neuronal entrenada y mantener su rendimiento tanto en datos conocidos como en datos nuevos (Han, Mao y Dally, 2016). Se pueden incluso «destilar» conjuntos de redes neuronales y crear una red más pequeña sin incurrir en pérdidas notables de rendimiento (Hinton, Vinyals y Dean, 2014). En algunos casos, la extensión de la poda o la compresión es sorprendente: hasta cien veces menor, dependiendo del conjunto de datos y la arquitectura de la red.

«Si los datos no son completamente aleatorios, las redes neuronales son capaces de extrapolar sus recuerdos a casos nuevos y generalizar»

Las consecuencias prácticas de la posibilidad de comprimir redes neuronales de forma considerable son obvias, especialmente cuando se necesita implementar dichas redes en dispositivos con pocos recursos, como los teléfonos móviles, o sistemas con hardware limitado, como los automóviles. Pero además de las consideraciones prácticas, también plantea varias preguntas: ¿Necesitamos una red de gran tamaño en primer lugar? ¿Existe algún giro arquitectónico que, combinado con los algoritmos actuales de búsqueda de mínimos, nos permita descubrir combinaciones de parámetros útiles para esas redes pequeñas? ¿O solo es cuestión de descubrir nuevos algoritmos de búsqueda de mínimos?

El aprendizaje se ve influido por la inicialización y el orden de los ejemplos

Como ocurre con el aprendizaje humano, el aprendizaje de las redes actuales depende del orden en el que se presentan los ejemplos. Los expertos saben que ordenar la muestra de diferente forma produce rendimientos diferentes y, en especial, que los primeros ejemplos influyen más en la precisión final (Erhan et al., 2010). Es más, un truco que se ha convertido en todo un clásico es entrenar previamente una red neuronal de forma no supervisada o transferir conocimiento de una tarea relacionada para beneficiarse de recursos adicionales (Yosinski, Clune, Bengio y Lipson, 2014). Además, es fácil demostrar que, aunque las inicializaciones aleatorias de los pesos de las redes convergen en una buena solución, cambiar las distribuciones de pesos iniciales o los parámetros de las distribuciones puede afectar a la precisión final o, en el peor de los casos, hacer que la red no aprenda nada (LeCun, Bottou, Orr y Müller, 2002). Aún queda mucho por aprender sobre los esquemas de inicialización con base matemática y sobre los órdenes óptimos de las muestras de entrenamiento. Parece difícil encontrar una teoría general. Además, como la variedad de arquitecturas de redes neuronales crece continuamente, a las teorías individuales con base matemática les resulta difícil mantenerse al día.

Tanto las redes neuronales artificiales como la mente humana pueden verse desconcertadas por los «ejemplos adversarios», imágenes que identificamos como algo (o parte de algo) y que después descubrimos que es otra cosa. La diferencia es que en el caso de las redes artificiales, estas pueden clasificar erróneamente una imagen tan solo al aplicarle una pequeña variación casi imperceptible. En la imagen, montaje inspirado en el meme «¿Chihuahua o magdalena?» que cobró popularidad en 2016 como ejemplo de las confusiones que pueden afectar a las redes neuronales de inteligencia artificial. / Mètode

Las redes neuronales pueden olvidar lo que aprenden

En contraste con los seres humanos, las redes neuronales olvidan lo que aprenden. Este fenómeno se conoce como interferencia catastrófica u olvido catastrófico, y se ha estudiado desde principios de los noventa (McCloskey y Cohen, 1989). Básicamente, cuando una red neuronal a la que se ha entrenado para realizar una tarea concreta es reutilizada para aprender una nueva tarea, esta olvida completamente cómo realizar la primera. Más allá del objetivo relativamente filosófico de imitar el aprendizaje humano y la cuestión de si las máquinas deberían o no ser capaces de hacerlo, el problema del olvido catastrófico tiene consecuencias importantes para el desarrollo actual de sistemas que consideran un gran número de tareas (potencialmente multimodales), y para aquellos que apuntan hacia un concepto de inteligencia más general. De momento parece poco realista que estos sistemas sean capaces de aprender de todos los datos relevantes posibles al mismo tiempo o de forma paralela.

Al llarg dels anys hi ha hagut diversos intents de solucionar l’oblit catastròfic. Algunes de les estratègies més comunes inclouen l’ús de records, els assajos o «sons» paral·lels, estratègies d’atenció o restringir la plasticitat de les neurones (Serrà, Surís, Miron i Karatzoglou, 2018). En un sentit més general, el problema de l’oblit catastròfic pot provenir del mateix algoritme de retropropagació, que representa l’essència de l’entrenament actual de xarxes neuronals. Potser una solució elegant del problema requerisca replantejar-se completament el paradigma actual.

«Como ocurre con el aprendizaje humano, el aprendizaje de las redes actuales depende del orden en el que se presentan los ejemplos»

Conclusión

Es interesante ver que un campo de investigación como el aprendizaje profundo, que atrae muchísima atención (por parte de los académicos, la industria o los medios de comunicación), pueda presentar tantos avances y, a la vez, tantas situaciones desconcertantes. Parece que la vanguardia tecnológica sigue muy por delante de nuestra comprensión, y esta situación podría continuar durante años. Sin embargo, también podría ocurrir que un avance teórico menor obligue a cambiar el paradigma por otro que a la larga facilite una aproximación más formal y matemática al aprendizaje profundo. Hasta entonces, la exploración empírica seguirá siendo el camino y la herramienta principal para salvar la distancia entre la práctica y la comprensión, un recuerdo de la aproximación de un nuevo tipo de ciencia.