Estadística en física de partículas
Su papel en el descubrimiento del bosón de Higgs

La estadística ha representado un papel de enorme importancia en el desarrollo de la física de partículas, pionera de la llamada «gran ciencia». Su aplicación ha evolucionado a la par de los desarrollos tecnológicos, que han permitido pasar de registrar unos pocos centenares a miles de millones de «sucesos». Este artículo discute sobre cómo se ha resuelto el problema de la manipulación de estas cantidades masivas de datos y cómo se han utilizado las principales herramientas estadísticas desde los años 1990 para buscar señales cada vez más pequeñas ocultas entre un ruido de fondo cada vez mayor. Muchos experimentos en la historia de la física de partículas podrían ilustrar el papel desempeñado por la estadística, pero pocos lo pueden hacer con un descubrimiento, fruto de un esfuerzo tecnológico y colectivo colosales, de tanta repercusión científica como el del bosón de Higgs.
Palabras clave: estadística, Monte Carlo, p-valor, física de partículas, bosón de Higgs.
«El principio de la ciencia, la definición, casi, es la siguiente: la prueba de todo conocimiento es el experimento. El experimento es el único juez de lo científicamente “verdadero”. Pero, ¿cuál es el origen del conocimiento? ¿De dónde provienen las leyes que deben ser testeadas? El experimento, por sí mismo, ayuda a generar esas leyes, en el sentido que nos da pistas. Pero también se necesita imaginación para crear a partir de esas evidencias las grandes generalizaciones […], y luego vuelta al experimento para comprobar de nuevo si hemos hecho la suposición correcta.» (Feynman, 1963). De este modo el gran físico Richard Feynman resumía el papel de la experimentación en el método científico. Hoy día, inmersos en la era de la generación y manipulación de cantidades masivas de datos, lo que se conoce como macrodatos, la estadística es una herramienta fundamental para hacer ciencia. En genómica, cambio climático o física de partículas, los descubrimientos surgen sólo cuando los datos son vistos a través del riguroso prisma de la estadística, dado que la señal buscada, si existe, se encuentra oculta entre un ruido de fondo gigantesco.
«En la era de la generación y manipulación de cantidades masivas de datos, la estadística es una herramienta fundamental para hacer ciencia»
La física de partículas surge como disciplina propia hacia los años 1950, siendo pionera de la «gran ciencia», dado que requiere experimentos con grandes detectores y aceleradores de partículas, e infraestructuras de macrodatos, desarrollados por grandes colaboraciones. En este entorno la estadística ha representado un papel de enorme importancia, aunque se ha hecho sin unos fuertes vínculos con la comunidad estadística, una situación que en los últimos años ha mejorado considerablemente (Physics Statistics Code Repository, 2002, 2003, 2005, 2007, 2011).
Su campo de estudio son las «partículas elementales» que se han ido descubriendo y que, junto con las fuerzas que surgen entre ellas, configuran lo que conocemos como modelo estándar: 6 quarks (u, d, s, c, b, t); 6 leptones (electrón, muón, tau y sus neutrinos asociados); los bosones intermediarios de las interacciones fundamentales (el fotón para la interacción electromagnética, dos W y el Z para la débil, y los 8 gluones de la fuerte; la gravitatoria, mucho menos intensa, aún no ha sido incluida satisfactoriamente); y los dos centenares de hadrones constituidos por dos quarks (llamados mesones), tres (bariones), e incluso cuatro (tetraquarks, cuyas evidencias van siendo cada vez más convincentes; Swanson, 2013; Aaij et al., 2014). A esta lista hay que añadir sus correspondientes parejas de antimateria: antiquarks, antileptones y antihadrones. Y por supuesto, el flamante bosón de Higgs, manifestación del campo de Englert-Brout-Higgs que inunda el vacío y es responsable de dotar de masa a todas ellas (excepto el fotón y los gluones, que no tienen), descubierto en 2012 tras haber sido postulado unos cincuenta años antes (Schirber, 2013). A todo esto hay que añadir lo que aún no se ha descubierto, como partículas supersimétricas, materia oscura, etc. La lista sólo está limitada por la imaginación de los teóricos que las proponen. Sin embargo, aunque se desconozca la naturaleza de esta «nueva física», existen poderosas razones que hacen pensar en su existencia real, por lo que las búsquedas continúan (Ellis, 2012).
Las preguntas a responder para cada tipo de partícula son muy variadas: ¿Existe? Si existe, ¿cuáles son sus propiedades (masa, espín, carga eléctrica, vida media, etc.)? Si no es estable, ¿qué partículas produce cuando se desintegra? ¿Cuáles son las probabilidades de los diferentes modos de desintegración? ¿Cómo son las distribuciones de energías y direcciones de las partículas del estado final? ¿Están de acuerdo con los modelos teóricos? ¿Qué procesos ocurren y con qué secciones eficaces (probabilidades) cuando colisiona con otra partícula? ¿Se comporta del mismo modo su antipartícula?
Para estudiar un cierto fenómeno se requiere, en primer lugar, producirlo eliminar «en condiciones controladas». Para ello suelen usarse haces de partículas procedentes de un acelerador u otro origen, como fuentes radiactivas o rayos cósmicos, bombardeando un blanco fijo o enfrentándose entre ellos. El tipo y energía de las partículas que colisionan se escogen para maximizar la producción del fenómeno en cuestión. En la «frontera de energía» los aceleradores permiten acelerar las partículas a mayores energías con el fin de producir nuevas partículas, mientras que en la «frontera de luminosidad» su alta intensidad permite descubrir procesos considerados prohibidos o muy raros que pueden tener implicaciones fundamentales.
Consideremos el caso del Gran Colisionador de Hadrones (LHC) del CERN en Ginebra, que tras unos veinte años de diseño y construcción empezó a funcionar en el año 2009. En este acelerador se hacen colisionar protones a una energía de hasta 7 TeV por protón (1 TeV = billón de electronvoltios, eV). En términos cotidianos, 1 TeV es similar a la energía cinética de un mosquito. Lo que hace que esta energía sea tan elevada es que se encuentra concentrada en una región del tamaño de una billonésima parte de una mota de polvo. Para registrar lo que ocurre tras la colisión se han construido grandes detectores (ATLAS y CMS para estudios de frontera de energía, LHCb y ALICE para frontera de luminosidad, y otros más pequeños) constituidos por un amplio abanico de sensores con millones de canales electrónicos de lectura.
Macrodatos
«En el LHC, unos sistemas electrónicos ultra-rápidos deciden en tiempo real si la colisión es interesante y, en tal caso, se registra en discos duros para reconstruirla y analizarla posteriormente»
millones de veces por segundo. Cada una de estas colisiones produce una pequeña explosión en la que parte de la energía cinética de los protones se convierte en otras partículas. La mayoría son muy inestables y se desintegran produciendo una cascada de entre centenares y miles de partículas más ligeras y estables, que son las que se observan directamente en los detectores. Utilizando unas pocas características de estos restos, unos sistemas electrónicos ultrarápidos llamados triggers deciden en tiempo real si la colisión es interesante y, en tal caso, se registra en discos duros para reconstruirla y analizarla posteriormente. Estos sistemas de adquisición de datos (figura 1) reducen a unos centenares por segundo las colisiones que producen física de interés, lo que genera aproximadamente 1 petabyte (mil millones de megabytes) de datos «crudos» al año por experimento.
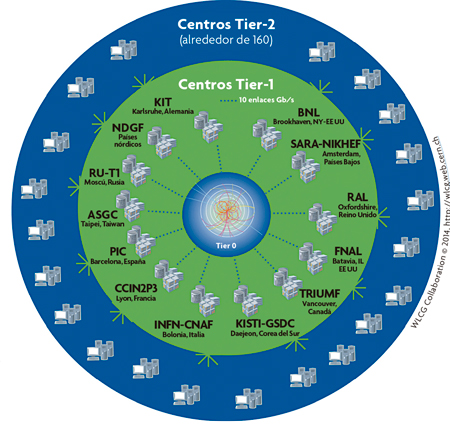
Figura 2. Diagrama de la distribución de los centros de cálculo de los experimentos del LHC (Tier). Los Tier-1, repartidos por Asia, Europa y América del Norte, están conectados por medio de conexiones específicas de hasta 10 gigabits por segundo al Tier-0 del CERN, mientras que los Tier-1 y Tier-2 están interconectados a través de las redes propias de investigación de los diferentes países. A su vez, todos los Tier están conectados a la red general de Internet. De este modo cualquier Tier-2 puede acceder a todos los datos. Esta infraestructura de almacenamiento de datos y de cálculo masivos se denomina Worldwide LHC Computing Grid (WLCG). El Tier-0 y los Tier-1 se dedican al (re)procesamiento de los datos reales, así como al almacenamiento permanente, tanto de datos reales como simulados. Los datos crudos sólo se almacenan en el Tier-0. Por su parte, los Tier-2 se dedican al almacenamiento parcial y temporal de datos, producciones de Monte Carlo, y procesamiento de las etapas finales de análisis de los datos.
En la fase de reconstrucción las señales electrónicas que constituyen los datos crudos se combinan e interpretan: los impactos que dejan las partículas a su paso por los sensores forman las trazas de sus trayectorias, se buscan intersecciones de éstas para identificar la posición de la colisión y los puntos de desintegración de las partículas inestables, la curvatura de las trayectorias en el seno de un campo magnético determina el momento, los calorímetros miden la energía de las partículas, etc. De este proceso de reconocimiento de patrones emerge el «suceso» reconstruido como una lista de partículas producidas con sus magnitudes cinemáticas medidas (energía, momento, posición y dirección) y en muchos casos su identidad. En los experimentos del LHC se ha desarrollado una infraestructura de almacenamiento y cálculo masivos denominada WLCG (Worldwide LHC Computing Grid) que permite distribuir la reconstrucción de los miles de millones de sucesos producidos anualmente entre centenares de miles de procesadores repartidos por todo el mundo (figura 2).
Conocido el patrón del fenómeno bajo estudio, durante la fase de análisis se realiza una clasificación o selección de sucesos (señal frente a ruido de fondo) utilizando técnicas de contraste de hipótesis. Con el reto de discriminar señales cada vez menores, los últimos años han sido testigos de cómo se han establecido y han evolucionado los métodos de clasificación multivariada basados en técnicas de aprendizaje (Webb, 2002). Ello no hubiera sido posible sin los importantes avances realizados por la comunidad estadística a la hora de combinar clasificadores y mejorar sus prestaciones. Para los sucesos seleccionados se evalúan, a partir de las variables cinemáticas asociadas a las partículas detectadas, las magnitudes físicas relevantes, y a continuación se representan gráficamente, usualmente en forma de diagrama de frecuencias (histograma).
Un ejemplo de este proceso de reducción de datos se ilustra en la figura 3, en cuya parte superior se muestra el histograma de la masa invariante de los pares de fotones que han superado el trigger, la reconstrucción y la clasificación como sucesos «candidatos» a bosones de Higgs producidos y desintegrados en dos fotones. La magnitud física en este caso, la masa invariante, se calcula a partir de la energía y dirección de los fotones medidas con los calorímetros. La reconstrucción completa de la colisión que da lugar a uno de estos candidatos se ilustra en la figura 4, en la que se identifican claramente los dos fotones sobre los cientos de trayectorias reconstruidas de otras partículas producidas en la colisión. Si los dos fotones proceden efectivamente de la producción y desintegración de una nueva partícula, el histograma debería presentar un exceso de sucesos localizado sobre un continuo de ruido de fondo, como así parece observarse. Es en la confrontación de esta distribución con la teoría cuando surgen las cuestiones estadísticas de interés: ¿Hay alguna evidencia del bosón Higgs? ¿Cuál es el mejor estimador de su masa, sección eficaz de producción y probabilidad de desintegración al estado final de dos fotones? ¿Son estos resultados compatibles con la predicción del modelo estándar?
Estadística y simulaciones de Monte Carlo
odo experimento en física de partículas puede entenderse como un experimento de contaje de sucesos. Así, para observar una partícula y medir su masa se hace uso de un histograma como el de la figura 3, en el que el número de sucesos N en cada intervalo de masa invariante es aleatorio y viene determinado por la distribución de Poisson, con desviación estándar √N (sólo en algunos casos particulares se hace preciso utilizar en su lugar estadística binomial, o gaussiana sin que se trate del límite para N grande). Esta aleatoriedad, sin embargo, no es consecuencia de un error de muestreo sino que está relacionada con la naturaleza cuántica de los procesos.
Las distribuciones predichas por la teoría suelen ser sencillas. Por ejemplo, las distribuciones angulares pueden ser uniformes o venir dadas por funciones trigonométricas, las masas suelen seguir una distribución de Cauchy (que los físicos de partículas llaman de Breit-Wigner), las distribuciones temporales pueden ser exponenciales o exponenciales moduladas por funciones trigonométricas o hiperbólicas. Estas formas sencillas se ven modificadas a menudo por efectos teóricos complejos, y siempre por la resolución, eficiencia y ruidos de fondo asociados a la reconstrucción de los sucesos.
Estas distribuciones se generan utilizando simulaciones de Monte Carlo. En primer lugar las partículas se generan siguiendo las distribuciones sencillas iniciales, incluyendo posteriormente las complicaciones teóricas. Para ello se ha desarrollado un elenco de generadores con nombres tan exóticos como Herwig, Pythia o Sherpa, que proporcionan una simulación completa de la dinámica de las colisiones (Nason y Skands, 2013). En segundo lugar se corrigen las distribuciones teóricas por la respuesta del detector, para lo que es necesario codificar un modelo virtual preciso de su geometría y composición en programas específicos, de los que el más sofisticado y extendido es Geant (Agostinelli, 2003). De este modo, la simulación del detector da cuenta de efectos tales como la interacción de las partículas con los materiales que éstas atraviesan, la cobertura angular, las regiones muertas, la existencia de canales electrónicos defectuosos o las imprecisiones en el posicionamiento de los dispositivos.
«La información simulada permite realizar una predicción completa de las distribuciones que siguen los datos reales. Los datos simulados, además, resultan fundamentales para la planificación de nuevos experimentos»
Uno de los problemas fundamentales de la simulación en sus diferentes fases es muestrear con alta eficiencia y máxima velocidad las funciones de densidad de probabilidad que definen las distribuciones. Para ello se usan generadores de números aleatorios uniformes de período largo o extremadamente largo. Cuando es posible calcular analíticamente la inversa de la función acumulativa, se muestrea la función de probabilidad con algoritmos específicos. Este es el caso de algunas funciones comunes como exponenciales, de Breit-Wigner o gaussianas. En caso contrario se emplea el método más general pero menos eficiente de Von Neumann (aceptación y rechazo).
La información simulada se utiliza para reconstruir las magnitudes cinemáticas con los mismos programas que se usan para los datos reales, lo que permite realizar una predicción completa de las distribuciones que siguen los datos. Por su complejidad y lentitud de ejecución, los programas de simulación absorben recursos de cálculo y almacenamiento de la infraestructura WLCG similares o incluso mayores que los de los datos reales (figura 2). Los datos simulados, además, resultan fundamentales para la planificación de nuevos experimentos.

Figura 4. Un suceso candidato a bosón de Higgs desintegrándose en dos fotones cuyas energías depositadas en los calorímetros del detector aparecen representadas por las «torres» rojas. Las líneas rectas discontinuas amarillas ilustran las direcciones de los fotones, definidas por el punto de colisión y las torres. Las líneas continuas amarillas representan las trayectorias reconstruidas de los cientos de otras partículas producidas en la colisión. La curvatura de estas trayectorias permite medir el momento de las partículas que las han producido, y es debida a la presencia de un campo magnético muy intenso. / CM Experiment © 2014 CERN
Estimación de parámetros físicos e intervalos de confianza
El conocimiento de las distribuciones teóricas, salvo unos pocos parámetros desconocidos, corregidas por el proceso de medida, implica que la función de verosimilitud es conocida y por tanto es posible obtener sus estimadores de máxima verosimilitud (Barlow, 1989; Cowan, 2013). Ejemplos de estimadores que pueden construirse a partir de la distribución de la figura 3 serían la masa de la partícula y la intensidad de la señal, esta última relacionada con el producto de la sección eficaz de producción y de la probabilidad de desintegración a dos fotones. Las correspondientes regiones de confianza para un nivel de confianza dado se obtienen a partir de la variación de la verosimilitud respecto de su valor máximo. En contadas ocasiones la solución es algebraica, lo que hace necesarias técnicas numéricas que, en el caso de problemas complejos con un gran volumen de datos, requieren importantes recursos computacionales. Una alternativa más económica utilizada tradicionalmente es el método de mínimos cuadrados, en el que se minimiza un test estadístico de tipo χ2. Su principal desventaja radica en asumir que los datos siguen una probabilidad gaussiana como aproximación a la distribución de Poisson, por lo que en general no se trata de un estimador de máxima verosimilitud, asintóticamente eficiente y sin sesgo. El método de máxima verosimilitud binado resuelve esta cuestión usando una verosimilitud de Poisson en cada intervalo en lugar del χ2. En este caso la eficiencia del estimador sólo se reduce si la anchura de los intervalos es mayor que la estructura de los datos. El incremento de la capacidad de los procesadores y el avance en protocolos de paralelización de los últimos años han permitido implantar el método de máxima verosimilitud completo.
Durante la última década también se ha generalizado el uso de la técnica de Toy Monte Carlo, también llamada de «falsos experimentos», para la obtención de regiones de confianza con la construcción de Neyman (Cowan, 2013). A partir de la función de verosimilitud se generan datos (falsos experimentos) para unos valores particulares de los parámetros. Cada uno de estos experimentos se ajusta para encontrar su estimador de máxima verosimilitud. Contando el número de experimentos con verosimilitud menor o mayor que la experimental, y explorando el espacio de parámetros, se encuentra la región de confianza con el deseado nivel de confianza. Esta técnica es fundamental cuando los datos no son correctamente descritos por distribuciones gaussianas, o la verosimilitud sufre distorsiones respecto de su esperado comportamiento asintótico o presenta máximos locales cercanos al máximo global. También es común aplicarla para certificar el contenido de probabilidad de regiones de confianza construidas con la aproximación gaussiana.
Significación estadística y descubrimiento
La probabilidad de que el resultado de un experimento sea consistente con una fluctuación aleatoria de los datos siendo cierta una determinada hipótesis (referida como hipótesis nula) se conoce como significación estadística o p-valor (Barlow, 1989; Cowan, 2013): cuanto menor sea mayor es la verosimilitud de que la hipótesis sea falsa. Para calcular p, generalmente con la técnica de Toy Monte Carlo, es preciso definir un test estadístico dependiente de los datos que refleje de algún modo el grado de discrepancia entre los datos y la hipótesis nula. Una implementación tipo es el cociente de verosimilitudes entre el mejor ajuste de los datos y el ajuste con la hipótesis nula. Es habitual convertir el p-valor en una significación equivalente Ζσ, utilizando para ello la distribución acumulativa de la distribución de Gauss normalizada. Desde los años 1990 los experimentos en física de partículas vienen utilizando un criterio mínimo de 5σ, correspondiente a un p-valor de 2,87 × 10-7, para excluir conclusivamente una hipótesis nula. Sólo en ese caso se habla de «observación» o «descubrimiento». El criterio es de unas 3σ, con un p-valor de 1,35 × 10-3, para «evidencia».
Estas exigencias resultan fundamentales cuando las medidas están sujetas a incertidumbres sistemáticas. Así, en las primeras décadas de la física de partículas los experimentos registraban, en el mejor de los casos, centenares de sucesos, con lo que las incertidumbres estadísticas eran tan elevadas que las sistemáticas resultaban despreciables. En los años 1970 y 1980 surgieron los detectores electrónicos y las incertidumbres estadísticas disminuyeron. Aún así, grandes descubrimientos de la época, como el del quark b (Herb et al., 1977), con una señal observada de unos 770 candidatos sobre un número esperado de sucesos con la hipótesis nula (ruido de fondo) de 350, o el del bosón W por el experimento UA1 (Arnison et al., 1983), con 6 sucesos observados sobre un ruido estimado despreciable, no evaluaron el nivel de significación de los hallazgos. En la actualidad se realizan análisis pormenorizados de este tipo de incertidumbres cuyo control requiere, por ejemplo, calibrar millones de canales de lectura del detector y afinar minuciosamente los datos simulados. Una tarea que en la práctica es compleja y que se propaga, en general, induciendo incertidumbres sistemáticas no despreciables
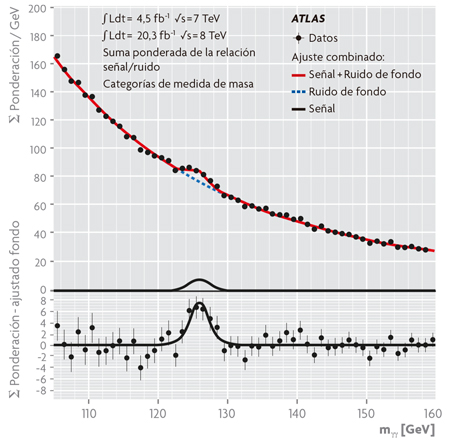
Figura 3. En la parte superior se muestra la distribución, en forma de histograma (puntos), de la masa invariante de los sucesos candidatos a bosones de Higgs producidos y desintegrados en dos fotones (Aad et al., 2012). Esta distribución se ha ajustado por el método de máxima verosimilitud a un modelo (línea continua roja) dado por la suma de una función de señal para una masa del bosón de 126,5 GeV (línea continua negra) y una función de ruido de fondo (línea discontinua azul). En la parte inferior se muestra la distribución de los datos (puntos) y del modelo ajustado (línea) después de haber sustraído la contribución del fondo. La suma cuadrática para todos los intervalos de la distancia de cada punto a la curva, normalizada a la correspondiente incertidumbre, define un test estadístico χ2 con el que se juzga la correcta descripción de los datos obtenida por el modelo. / Fuente: ATLAS Experiment © 2014 CERN.
La definición de la significación estadística en términos de un p-valor hace patente la importancia de la decisión a priori en la elección del test estadístico, dada la dependencia de éste de los propios datos con los que se pretende realizar la observación. Esta libertad de elección puede dar lugar a lo que se ha denominado p-hacking (Nuzzo, 2014). El riesgo de p-hacking radica en que el experimentador, incluso inconscientemente, monitoriza el experimento con los mismos datos con los que realiza la observación, introduciendo cambios en los criterios de selección y en las correcciones de las distribuciones hasta que obtiene el acuerdo deseado, y no hasta que considera que todas las modificaciones necesarias se han tenido en cuenta. Este modo de proceder puede inducir sesgos tanto en la estimación de los parámetros como en el propio p-valor. Aunque la física de partículas ha sido siempre cuidadosa, y prueba de ello es el hábito casi obsesivo de explicar los detalles de la selección de los datos, no ha dejado de verse afectada por este problema. Para eliminarlo es frecuente utilizar la técnica de «blindaje», en la que se definen los criterios de selección de los datos, las correcciones de las distribuciones y el test estadístico sin tener conocimiento de los datos, haciendo uso de datos simulados o muestras de datos reales en las que no se espera ninguna señal, o introduciendo un sesgo desconocido en los parámetros físicos a medir.
Con todo, el p-valor sólo se utiliza para determinar el grado de incompatibilidad entre los datos y la hipótesis nula, evitando hacer un uso abusivo como herramienta de inferencia sobre la naturaleza real del efecto. Además, el grado de convencimiento de la observación en base al p-valor también depende de otros factores tales como la confianza en el modelo que ha dado lugar al mismo y la existencia de múltiples hipótesis nulas con p-valores similares. Para ello hay que afrontar el problema de la falta de información en el método de máxima verosimilitud que permita juzgar la calidad del modelo que mejor describe los datos. La solución habitualmente adoptada es la de determinar el p-valor para un test estadístico χ2. Un test alternativo ocasionalmente utilizado es el de Kolmogorov-Smirnov (Barlow, 1998).
El bosón de Higgs
Estamos ahora en situación de intentar responder a las cuestiones estadísticas formuladas (Aad et al., 2012; Chatrchyan et al., 2012). Para ello, los datos que dan lugar al histograma de la figura 3 se ajustan por el método de máxima verosimilitud completo a un modelo constituido por la suma de una función paramétrica de señal fija para diferentes masas del bosón y otra de ruido de fondo. La descripción de la forma de la señal se ha obtenido a partir de simulaciones de Monte Carlo completas, mientras que la del fondo se ha efectuado usando los datos a ambos lados de la región donde se observa el exceso. Explorando para diferentes masas del bosón se ajusta la constante de normalización de la señal. Sustrayendo de la distribución de los datos y del modelo ajustado la contribución del fondo se obtiene la parte inferior de la figura. Las diferencias entre los puntos y la curva definen el test estadístico χ2 con el que se juzga la correcta descripción de los datos obtenida por el modelo. La técnica de blindaje en este caso ha consistido en ocultar la distribución de masa entre 110 y 140 GeV hasta concluir la fase de selección de los datos y optimización del análisis.
«Aunque el modelo estándar no predice la masa del bosón de Higgs, sí predice el producto de su sección eficaz de producción y la probabilidad de que se desintegre en un cierto estado final. Esta predicción resulta fundamental»
A continuación se determina la significación estadística del exceso de sucesos en la región cercana al mejor valor del estimador de la masa de la partícula. Para ello se calcula el p-valor con un test estadístico construido a partir del cociente de verosimilitudes entre el ajuste de la distribución de masa con y sin la componente de señal. Explorando para distintos valores de la masa y combinando con otros estados finales de desintegración analizados no discutidos aquí (dos y cuatro leptones, sean electrones o muones) se obtiene la curva continua de la figura 5. El menor p-valor, correspondiente a una significación estadística de 5,9σ, ocurre para una masa de 126,5 GeV, unas 130 veces mayor que la masa del átomo de hidrógeno. El correspondiente valor considerando sólo el estado final a dos fotones es 4,5σ. Estos resultados, junto con la correcta descripción de los datos obtenida por el modelo con señal, permiten refutar la hipótesis nula y obtener evidencia convincente del descubrimiento de la producción y desintegración de una partícula en dos fotones. Que la partícula sea un bosón (partícula con un valor entero del espín) se infiere directamente de su desintegración en dos fotones (a su vez bosones con espín 1).
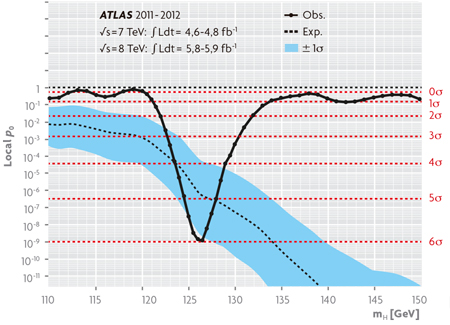
Figura 5. La curva continua (Obs.) representa el p-valor «observado» de la hipótesis nula (ausencia de señal) obtenido a partir de la variación de la verosimilitud del ajuste de la distribución de masa invariante de los sucesos candidatos a bosones de Higgs producidos y desintegrados en dos fotones (figura 3), dos leptones y cuatro leptones, con y sin la componente de señal, en función de la masa de los candidatos (Aad et al., 2012). La curva discontinua (Exp.) indica el p-valor «esperado» según las predicciones del modelo estándar, mientras que la banda en azul corresponde a su incertidumbre a 1σ. En la región entorno al mínimo del p-valor observado se aprecia que éste (curva continua) es inferior al valor central del correspondiente p-valor esperado (curva discontinua) aunque compatible con el intervalo de confianza a 1σ (banda). Dado que el p-valor es menor cuanto mayor sea la intensidad de la señal, se concluye que los datos no excluyen que la señal sea debida al bosón de Higgs del modelo estándar. Las líneas horizontales representan los p-valores correspondientes a niveles de significación estadística de 1 a 6σ. Los puntos sobre la línea continua son los valores específicos de la masa del bosón utilizados para la simulación de la señal con los que se ha obtenido la curva por interpolación. / Fuente: ATLAS Experiment © 2014 CERN.
Otra cuestión es establecer la naturaleza real de la observación, empezando por si estamos o no ante el bosón de Higgs del modelo estándar. Aunque el modelo estándar no predice su masa, sí predice, en función de ésta, el producto de su sección eficaz de producción y la probabilidad de que se desintegre en un cierto estado final. Esta predicción resulta fundamental, ya que, con la ayuda de las simulaciones de Monte Carlo, permite establecer la señal que se espera con su incertidumbre y los correspondientes p-valores en términos de la masa, como se muestra en la curva discontinua y la banda azul de la figura 5. La comparación entre la curva continua y la banda indica que la intensidad de la señal observada es compatible con la esperada a 1σ (p-valor de 0,317, o equivalentemente, un contenido de probabilidad del 68,3%), y por tanto no se excluye que se trate del bosón de Higgs del modelo estándar. Con el cociente entre las dos intensidades se construye un nuevo test estadístico que, al explorarse en función de la masa, permite obtener el mejor estimador de la masa de la nueva partícula y su intervalo de confianza a 1σ, 126.0 ± 0.4 ± 0.4 GeV, donde el segundo (tercer) valor denota la incertidumbre estadística (sistemática). Estudios similares realizados analizando la distribución angular de los fotones y leptones, magnitud física sensible al espín y la paridad (otra propiedad cuántica que toma valores + y –) del bosón, han permitido excluir con p-valores menores de 0,022 asignaciones de espín-paridad 0–, 1+, 1–, 2+ frente a la asignación 0+ predicha por el modelo estándar (Aad et al., 2013; Chatrchyan et al., 2013).
Con toda esta información no podemos concluir sin riesgo de abusar de la ciencia estadística que se trata del bosón de Higgs del modelo estándar, pero ciertamente se le parece mucho.
Agradecimientos:
El autor agradece a los profesores Santiago González de la Hoz y Jesús Navarro Faus, así como a los revisores anónimos, por sus comentarios y aportaciones a este manuscrito.
Referencias
Aad, G. et al., 2013. «Observation of a New Particle in the Search for the Standard Model Higgs Boson with the ATLAS Detector at the LHC». Physics Letters B, 716(1): 1-29. DOI: <10.1016/j.physletb.2012.08.020>.
Aad, G. et al., 2013. «Evidence for the Spin-0 Nature of the Higgs Boson Using ATLAS Data». Physics Letters B, 726(1-3): 120-144. DOI: <10.1016/j.physletb.2013.08.026>.
Aaij, R. et al., 2014. «Observation of the Resonant Character of the Z(4430)– State». Physical Review Letters, 112: 222002. DOI: <10.1103/PhysRevLett.112.222002>.
Agostinelli, S. et al., 2003. «Geant4-a Simulation Toolkit». Nuclear Instruments and Methods in Physics Research A, 506(3): 250-303. DOI: <10.1016/S0168-9002(03)01368-8>.
Arnison, G. et al., 1983. «Experimental Observation of Isolated Large Transverse Energy Electrons with Associated Missing Energy at √s=450 GeV». Physics Letters B, 122(1): 103-116. DOI: <10.1016/0370-2693(83)91177-2>.
Barlow, R. J., 1989. Statistics. A Guide to the Use of Statistical Methods in the Physical Sciences. John Wiley & Sons. Chichester (Inglaterra).
Chatrchyan, S. et al., 2012. «Observation of a New Boson at a Mass of 125 GeV with the CMS Experiment at the LHC». Physics Letters B, 716(1): 30-61. DOI: <10.1016/j.physletb.2012.08.021>.
Chatrchyan, S. et al., 2013. «Study of the Mass and Spin-Parity of the Higgs Boson Candidate via Its Decays to Z Boson Pairs». Physical Review Letters, 110: 081803. DOI: <10.1103/PhysRevLett.110.081803>.
Cowan, G., 2013. «Statistics». En Olive, K. A. et al., 2014. «Review of Particle Physics». Chinese Physics C, 38(9): 090001. DOI: <10.1088/1674-1137/38/9/090001>.
Ellis, J., 2012. «Outstanding Questions: Physics Beyond the Standard Model». Philosophical Transactions of The Royal Society A, 370: 818-830. DOI: <10.1098/rsta.2011.0452>.
Feynman, R. P., 1963. The Feynman Lectures on Physics. Addison-Wesley. Reading, Massachusetts.
Herb, S. W. et al., 1977. «Observation of a Dimuon Resonance at 9.5 GeV in 400-GeV Proton-Nucleus Collisions». Physical Review Letters, 39: 252-255. DOI: <10.1103/PhysRevLett.39.252>.
Nason, P. y P. Z. Skands, 2013. «Monte Carlo Event Generators». En Olive, K.A. et al., 2014. «Review of Particle Physics». Chinese Physics C, 38(9): 090001. DOI: <10.1088/1674-1137/38/9/090001>.
Nuzzo, R., 2014. «Statistical Errors». Nature, 506: 150-152. DOI: <10.1038/506150a>.
Physics Statistics Code Repository, 2002; 2003; 2005; 2007; 2011. Congreso PHYSTAT 2002. Durham. Disponible en: <http://phystat.org>.
Schirber, M., 2013. «Focus: Nobel Prize-Why Particles Have Mass». Physics, 6: 111. DOI: <10.1103/Physics.6.111>.
Swanson, E., 2013. «Viewpoint: New Particle Hints at Four-Quark Matter». Physics, 6: 69. DOI: <10.1103/Physics.6.69>.
Webb, A., 2002. Statistical Pattern Recognition. John Wiley & Sons. Chichester (Anglaterra).





