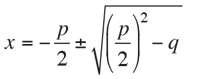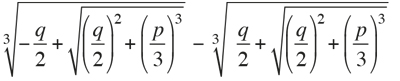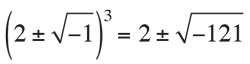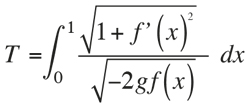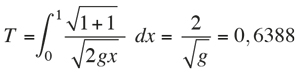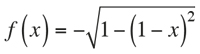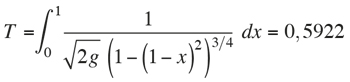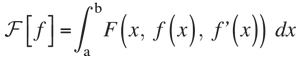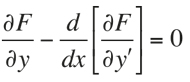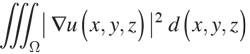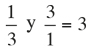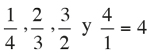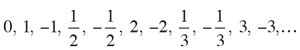Antiguos retos matemáticos
Antecedentes de los problemas del milenio

Los problemas del milenio del Instituto Clay de Matemáticas son un estímulo para la investigación matemática. El objetivo de este artículo es mostrar algunos precedentes de retos que también han representado estímulos para demostrar resultados interesantes. Con esta excusa, mostramos tres momentos de la historia de la matemática que han sido importantes para desarrollar nuevas líneas de investigación. Analizamos brevemente el desafío de Tartaglia, que significó conocer una fórmula para la ecuación de tercer grado; el problema de la curva de descenso más rápido de Johann Bernoulli, que dio origen al cálculo de variaciones; y la incidencia de los problemas que planteó David Hilbert en 1900, centrándonos en el primer problema de su lista: la hipótesis del continuo.
Palabras clave: ecuación cúbica, fórmula de Cardano-Tartaglia, braquistócrona, problemas de Hilbert, hipótesis del continuo.
El Instituto Clay de Matemáticas ha elegido siete problemas matemáticos y ofrece un millón de dólares a quien resuelva alguno. Como eso de plantear retos matemáticos no es algo inédito, en este artículo queremos mostrar varios desafíos que han tenido lugar a lo largo de la historia. No incluimos controversias como la de Newton-Leibniz, la de D’Alembert-Bernoulli o la de Cantor-Kronecker. Asimismo, dejaremos aparte los premios que han convocado las academias de ciencias (como la de Francia o la de Prusia desde el siglo XVIII).
Mostraremos, pues, ciertos aspectos del desarrollo de las matemáticas desde una perspectiva especial. Referencias clásicas en historia de la matemática son Carl Benjamin Boyer (1989) y Morris Kline (1972). Otro libro, más divulgativo, es obra de William Wade Dunham (1990). Además, una fuente muy valiosa de material histórico (fundamentalmente biografías) es el sitio web de la Universidad de St. Andrews (Escocia).
El desafío de Tartaglia
Ya los antiguos matemáticos de Mesopotamia formularon una serie de instrucciones (sin ninguna explicación) para encontrar soluciones concretas a problemas que hoy se pueden describir mediante una ecuación de segundo grado. Hablando en términos modernos, si la incógnita verifica la ecuación , entonces la solución viene dada por:
Hay que decir que no solo hemos utilizado la notación moderna; el lenguaje empleado es más bien una licencia, porque en la antigüedad p y q son siempre cantidades positivas y se buscan soluciones positivas.
«Ya los antiguos matemáticos de Mesopotamia formularon una serie de instrucciones para encontrar soluciones concretas a problemas que hoy se pueden describir mediante una ecuación de segundo grado»
En principio, la ecuación puede tener asociado el cálculo de un área, por eso aparece el cuadrado. Por tanto, tiene sentido considerar ecuaciones de tercer grado asociadas al cálculo de volúmenes. Efectivamente, la ecuación cúbica se planteó e, incluso, fue resuelta geométricamente. Este resultado se debe al matemático persa Omar Khayyam (1048-1131), quien utilizaba secciones cónicas (es decir, elipses, parábolas e hipérbolas) cuya intersección proporcionaba las raíces. Por otro lado, con paciencia, siempre se pueden aproximar las raíces de cualquier polinomio. Por ejemplo, Leonardo de Pisa (ca. 1170-1250), también llamado Fibonacci, expresó de manera aproximada la raíz de una ecuación cúbica. El caso es que al final de la época medieval ya había métodos para calcular geométrica o aproximadamente raíces de ecuaciones cúbicas. Sin embargo, no se conocía ninguna expresión para obtenerlas y, a juicio del influyente Luca Pacioli (1445-1517), eso de encontrar una fórmula para una ecuación general de tercer grado era tan difícil como cuadrar un círculo.

Niccolò Fontana, de mote Tartaglia, explicó a Girolamo Cardano cómo resolver las ecuaciones de tercer grado, bajo la promesa de mantener la regla en secreto. Pero Cardano no cumplió el compromiso y en 1545 publicó la fórmula en el libro Ars Magna. / Mètode
La disputa con la ecuación cúbica como tema fundamental se produjo en 1535. En aquel tiempo se celebraban muchos desafíos con apuestas. Uno de los protagonistas de la disputa era Niccolò Fontana (1500-1557), de mote Tartaglia (“tartamudo”). Llegó a Venecia en 1534 y ganó fama de buen matemático. Parece que decía que podía resolver algunos casos concretos de la cúbica. Es entonces cuando Antonio Maria del Fiore retó a Tartaglia. Cada contrincante propuso una lista de treinta problemas para solucionar en un intervalo de tiempo fijo, y aquel que resolviese menos pagaría una comida a tantos amigos del ganador como problemas hubiera solucionado éste. La cuestión es que Del Fiore conocía una fórmula para resolver una clase de ecuaciones de tercer grado, que le había desvelado Scipione del Ferro (1465-1526) poco antes de morir. Por ello, todos los problemas que propuso a Tartaglia eran ecuaciones cúbicas incompletas. Tartaglia comprendió que Del Fiore tenía una fórmula y la buscó hasta descubrirla. El día en que se decidía el resultado, Tartaglia había solucionado todos los problemas propuestos por Del Fiore, mientras que éste no había resuelto ninguno.
En términos actuales, la ecuación cúbica que estudió Tartaglia era , aunque él siempre escribía números en lugar de los coeficientes p y q. La solución viene dada por la fórmula de Cardano-Tartaglia, según la cual x es igual a:
Después de la disputa era evidente para todo el mundo que Tartaglia disponía de una regla para la cúbica, pero no la publicó. En aquel momento apareció Girolamo Cardano (1501-1576) presionando a Tartaglia para que le dijese cómo resolver las ecuaciones de tercer grado. Finalmente Tartaglia le comunicó la regla en clave, bajo la promesa de mantenerla en secreto. Cardano no cumplió su promesa y en 1545 publicó la fórmula en el libro Ars Magna. Además de la solución de Tartaglia, aparece la regla para encontrar una solución de la ecuación general , que Cardano había obtenido en colaboración con su discípulo Ludovico Ferrari (1522-1565). Más sorprendente es que en el libro se encontraba la solución de una ecuación general de cuarto grado; la había descubierto Ferrari con técnicas parecidas a las que habían aprendido para resolver la cúbica.
Todas estas investigaciones son el punto de partida de dos líneas de investigación matemática. Por una parte, empezó a plantearse encontrar una fórmula para la ecuación de quinto grado. Después de los esfuerzos de un buen puñado de matemáticos a lo largo de más de dos siglos, entre los que hay que destacar a Joseph-Louis Lagrange (1736-1813), el noruego Niels Abel (1802-1829) demostró que era imposible encontrar la solución general de una ecuación de grado mayor que cuatro mediante radicales. La historia no se acaba porque aún faltaba saber cuándo es posible esta solución por radicales. Poco antes de morir en un duelo, Évariste Galois (1811-1832) hizo un escrito en el que probaba una teoría de la solubilidad: establecía un criterio para, dada una ecuación de grado primo, saber si es o no resoluble por radicales. La publicación de este escrito de Galois en 1846 puede considerarse el punto de partida del álgebra moderna.
«La publicación de un escrito de Évariste Galois en 1846 puede considerarse el punto de partida del álgebra moderna»
Por otra parte, hay un caso muy importante en la fórmula de la ecuación cúbica que es el que aparece cuando (q/2)2 + (p/3)3 < 0. Cardano y Ferrari lo llamaron «caso irreductible». Es sabido que la ecuación cúbica siempre tiene raíces. ¿Qué pasa si aplicamos la fórmula también en este caso? Simplemente aparecen expresiones que involucran raíces cúbicas y cuadradas de números negativos. Por ejemplo, supongamos que ya sabemos que una raíz de es x = 4, pero intentemos aplicar la regla, entonces obtendremos:
Haciendo substituciones formales se puede deducir que:
Y por consiguiente llegamos a:
La cuestión que pone de manifiesto este cálculo es que la manipulación de raíces cuadradas de números negativos puede ser útil. Es el origen de los números complejos. Asimismo, Cardano y Ferrari se dieron cuenta de que, utilizando estos números extraños, toda ecuación cúbica tiene tres raíces y toda ecuación cuártica tiene cuatro. Es la versión inicial del llamado «teorema fundamental del álgebra»: todo polinomio de grado n tiene n raíces complejas (teniendo en cuenta las raíces repetidas). Más adelante, la investigación en números complejos dará lugar a la teoría de funciones de variable compleja, cuyas propiedades son muy diferentes de las funciones de variable real (por ejemplo, toda función derivable en un disco se puede representar por una serie de potencias).

Podríamos decir que la curva de descenso más rápido es la que permite hacer el diseño óptimo de un tobogán. Dejando caer bolas por un plano inclinado y por una circunferencia, Galileo Galilei se dio cuenta de que el descenso era más rápido por la segunda. En la imagen, aparato fabricado por Francesco Spighi que permite comparar la caída de una bola por una cicloide y por una recta. Se puede contemplar en el Museo Galileo de Florencia. / Sailko/Wikimedia
La curva de descenso más rápido
Uno de los precursores del cálculo diferencial, Pierre de Fermat (1601-1665), descubrió un método para calcular máximos y mínimos: actualmente diríamos que si un punto x es máximo o mínimo de una determinada función suave f entonces verifica f’(x) = 0. Este método lo aplicó al estudio de los rayos de luz, junto al principio que afirma que la luz viaja entre dos puntos recorriendo el camino que requiere menos tiempo. Así dedujo la ley de la reflexión y de la refracción (ley de Snell), la última suponiendo que la luz se mueve más despacio en un medio más denso. Es significativo que la misma ley de Snell fue utilizada más tarde por Johann Bernoulli (1667-1748), considerando un medio óptico no homogéneo consistente en capas paralelas superpuestas horizontalmente de densidad variable, para encontrar la curva de descenso más rápido. La idea era que la luz en este medio fuera precisamente por la curva que buscaba y que llamó «braquistócrona».
¿Cuál es la curva de descenso más rápido? La definición formal es la siguiente: dados dos puntos A y B en un plano vertical de forma que A esté a más altura que B, la curva de descenso más rápido es la que sigue un peso puntual cuando se desplaza de A a B en el menor tiempo posible bajo el efecto de la gravedad. En otras palabras, la curva de descenso más rápido es la que permite hacer el diseño óptimo de un tobogán. La primera idea que se puede tener es que la curva es en realidad una recta porque la recta es la curva más corta entre dos puntos. Pero Galileo Galilei (1564-1642) se dio cuenta de que esto no era así, ya que al dejar caer bolas por un plano inclinado y por una circunferencia observó que el descenso por la circunferencia era más rápido.
Para hacernos una idea de la cuestión, consideremos los puntos A = (0,0) y B = (1,–1). Queremos averiguar, entre todas las funciones y = f(x) que verifican f(0) = 0 y f (1) = –1, aquella que hace mínimo el tiempo de caída de un peso (T) que sigue la gráfica de la función. Por un razonamiento físico se llega a la cantidad que hay que minimizar, que es:
donde g denota la constante de la gravedad. Ahora seguiremos a Galileo y calcularemos el tiempo empleado a lo largo de varias curvas. Para la recta f(x) = –x, obtenemos
para el arco de circunferencia
obtenemos
Es decir, Galileo tenía razón. Ahora bien, tampoco la circunferencia es la braquistócrona porque, en realidad, el mínimo se alcanza cuando T = 0,5832.
En las páginas de la revista alemana Acta Eruditorum de junio de 1696, Johann Bernoulli propuso a la comunidad matemática el reto de encontrar la braquistócrona. Él afirmaba que conocía la respuesta y que se trataba de una curva bien conocida por los geómetras. En mayo de 1697, Bernoulli publicó que cuatro matemáticos habían conseguido una prueba de que la braquistócrona era la cicloide; es decir, la curva que viene definida por un punto de una circunferencia que gira sin deslizar sobre una línea recta (por ejemplo, un punto del neumático de la rueda de un coche sobre la calle). Eran Gottfried Wilhelm Leibniz, Jakob Bernoulli, el marqués de L’Hôpital Guillaume François Antoine y un matemático anónimo; cada uno había hecho una demostración diferente.
El escrito del desafío parecía una invitación especialmente dirigida a Isaac Newton (1643-1727), por lo que no es sorprendente que tuviese que responder al reto. Corre una leyenda que dice que recibió el problema cuando volvía, cansado, de trabajar todo el día en la casa de la moneda y se concentró durante doce horas hasta resolverlo: es el problema que le costó toda una noche a Newton. La respuesta la envió anónimamente, pero Bernoulli al verla adivinó el autor y exclamó que sabía que era de Newton como conocía «al león por sus garras».
El problema de la braquistócrona es uno de los primeros ejemplos de lo que después se convertiría en cálculo de variaciones. Se trata de minimizar una cantidad, en nuestro caso el tiempo, que no depende de un número finito de variables independientes sino de la forma global de la curva. Un problema típico de cálculo de variaciones es encontrar la función que minimiza una integral como
para una cierta función F(x, y, y’). Lo que se puede pensar es aplicar la idea de Fermat, de quien ya hemos hablado: derivar (de alguna forma) la función F y hacer F’[f] = 0 para obtener una condición sobre la función f. Los estudios de Leonhard Euler (1707-1783) y Joseph-Louis Lagrange (1736-1813) descubrieron que este procedimiento llevaba a la condición:
Los razonamientos, sin embargo, no eran rigurosos y tenemos que esperar al siglo XIX para tener un fundamento satisfactorio del cálculo de variaciones de la mano de Karl Weierstrass (1815-1897) y David Hilbert (1862-1943).
Mientras tanto, los matemáticos habían planteado problemas de minimización de integrales múltiples, como las de la teoría del potencial que busca minimizar la integral
entre todas las funciones u, con derivadas parciales continuas, que verifican una condición en la frontera del dominio Ω. Por su parte, los físicos habían aplicado las ideas del cálculo de variaciones a la mecánica y así surgió la mecánica analítica con las formulaciones lagrangiana y hamiltoniana. Por debajo flotaba una generalización de la idea de Fermat: la naturaleza economiza en sus acciones y, consecuentemente, en todos los fenómenos naturales existe una cantidad (o cantidades) que tiene que ser minimizada.

En 1900 el matemático David Hilbert propuso una lista de veintitrés problemas no resueltos de todos los campos de la matemática como ejemplos de cuestiones que serían fundamentales en el siglo que empezaba. En la imagen, Hilbert –fila de delante, a la derecha– con unos amigos. / Yeshiva University
Los veintitrés problemas de Hilbert
En el verano de 1900, David Hilbert estaba casi en el cenit de su carrera académica. Su currículo contenía la solución al problema de Gordon sobre invariantes de ciertas formas algebraicas, el nuevo impulso que había dado a la teoría algebraica de números, la axiomatización de la geometría o la justificación del principio de Dirichlet bajo ciertas hipótesis. Era uno de los más reputados matemáticos de la época. Y en aquel momento impartió una conferencia en el Segundo Congreso Internacional de Matemáticos celebrado en París.
En la conferencia titulada «Problemas matemáticos» (se puede consultar en Hilbert, 1902) puso de manifiesto su filosofía de las matemáticas, llena de optimismo. Además, propuso una lista de veintitrés problemas no resueltos de todos los campos de la matemática como ejemplos de cuestiones que serían fundamentales en el siglo que empezaba. La lista concentró los esfuerzos de numerosos matemáticos y llegó a ser muy influyente (sin duda por la autoridad de Hilbert). En resumen, aquel que resolvía uno de los problemas, alcanzaba una sólida reputación.
«Una parte considerable del desarrollo matemático del siglo XX tiene como origen la lista de problemas de David Hilbert»
Las matemáticas del nuevo siglo no siguieron exactamente las líneas de investigación marcadas por Hilbert. Incluso él no pudo adivinar las nuevas áreas que aparecieron muy pronto y que, en algunos casos, el propio Hilbert ayudó a desarrollar, como la teoría espectral. Sin embargo, una parte considerable del desarrollo matemático del siglo XX tiene como origen la lista de Hilbert. Haremos una breve introducción al primer problema de la lista en la siguiente sección.
La hipótesis del continuo
A finales del siglo XIX, Georg Cantor (1845-1918) analizó el infinito de forma sistemática. En su teoría, dos conjuntos (finitos o infinitos) tienen el mismo cardinal si existe una biyección entre ellos. Observen que, cuando el conjunto es finito, su cardinal es el número de elementos que tiene.
Aplicando su definición a los conjuntos N, de todos los enteros positivos, y Q, de todos los números racionales (los que se pueden escribir como m/n, donde m y n son enteros, y n ≠ 0), probó que ambos tienen el mismo cardinal. Se trata del cardinal infinito más pequeño que denotó por ℵ0. Cuando un conjunto tiene cardinal ℵ0 como existe una biyección con los enteros positivos, los miembros del conjunto se pueden escribir como una sucesión. No es demasiado difícil entender la demostración que el cardinal de Q es ℵ0 cuando se conoce el procedimiento. Consideremos números racionales m/n que sean una fracción irreductible con m y n positivos y tales que la suma m + n es una cantidad fija. Si m + n = 2, entonces tenemos:
Si m + n = 3, tenemos:
Si m + n = 4, tenemos:
Si m + n = 5, tenemos:
Es evidente que, continuando el proceso para m + n = 6, 7,… incluiremos todos los números racionales positivos.
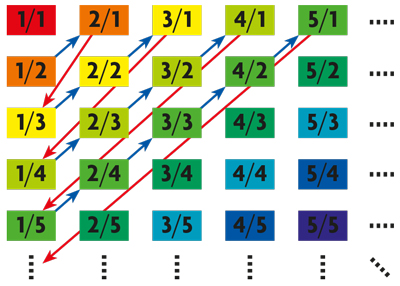
Proceso para expresar los racionales positivos como una sucesión. / Sergio Segura
Hay que incluir también el 0 y los negativos, por lo que los intercalaremos entre los positivos. Los primeros términos de la sucesión que contiene todos los números racionales son:
Posteriormente Cantor demostró que el conjunto de todas las raíces de polinomios con coeficientes enteros tiene el mismo cardinal.
La cuestión cambió cuando vio que el conjunto R de los números reales (aquellos que se pueden escribir con decimales aunque sean irracionales) es mayor que ℵ0. La demostración se hace por reducción al absurdo. Cantor supuso que todos los números entre 0 y 1 se podían escribir en una sucesión y encontró un número que no era de la sucesión. Quizá este es el primer teorema significativo de su teoría, el cual muestra que existen diferentes tipos de infinito. Consecuencia de este hecho es que la mayoría de los números reales son irracionales. Más aún, la mayoría de los números reales no son raíces de ningún polinomio con coeficientes enteros. Teniendo en cuenta que se conocían pocos números de este tipo, el resultado fue muy sorprendente para la época.
Profundizando en su análisis, demostró que hay tantos números reales como subconjuntos de N. Sin embargo, no encontró ningún conjunto que tuviese un cardinal mayor que ℵ0 y menor que el de R. Así llegó a la conjetura de que el cardinal de R era el segundo cardinal infinito; es la hipótesis del continuo, cuyo enunciado es: cualquier subconjunto infinito del conjunto de los números reales se puede poner en biyección con el conjunto de los números naturales o con el propio conjunto de los reales.
Durante los años siguientes, se hicieron numerosos esfuerzos para intentar demostrar la conjetura de Cantor sin éxito y Hilbert lo puso como el primer problema de su lista. La solución vino poco a poco, y no es una solución fácil de entender.
El primer paso lo dio Kurt Gödel (1906-1978). En 1940 demostró que si el sistema axiomático habitual de la teoría de conjuntos es consistente, entonces continuará siendo así cuando la hipótesis del continuo se agregue al sistema. En otras palabras, la hipótesis del continuo no es contradictoria con el resto de axiomas que se consideran en teoría de conjuntos. Por tanto, no se puede descubrir un conjunto que tenga un cardinal mayor que ℵ0 y menor que el de R porque se llegaría a una contradicción. Pero eso no es una demostración de la hipótesis del continuo.
El segundo paso se debe a Paul Joseph Cohen (1934-2007), quien en 1963 demostró que de hecho la hipótesis del continuo es independiente de los otros axiomas. En efecto, utilizando un método que llamó «forcing», vio que si el sistema axiomático de la teoría de conjuntos es consistente, entonces lo continuará siendo cuando la negación de la hipótesis del continuo se agregue al sistema. La conclusión es que ni la hipótesis del continuo ni su negación se pueden demostrar con el sistema axiomático habitual de la teoría de conjuntos. Podemos añadir otro axioma que dice que la hipótesis del continuo es cierta (o añadir uno negándola). Con los axiomas actuales tenemos un desconocimiento total de la cuestión.
De acuerdo con Gödel, el problema no se acaba aquí. Lo que hemos visto es que los axiomas de la teoría de conjuntos son insuficientes para responder a la cuestión y tienen que ser complementados con otros. En el futuro, los matemáticos añadirán al sistema nuevos axiomas. El criterio para añadirlos será que tendrán consecuencias deseables (según nuestra intuición de matemáticos) y no tendrán consecuencias no deseables. Gödel pensaba que la conjetura de Cantor era falsa. Con los nuevos axiomas se podrá volver a formular el problema de la hipótesis del continuo.
Más allá de los problemas de Hilbert
La conferencia de Hilbert tuvo tal repercusión que, para conmemorarla, la Unión Matemática Internacional declaró el 2000 como Año Internacional de las Matemáticas y pidió listas de problemas a prestigiosos matemáticos, como Stephen Smale, quien sugirió dieciocho problemas. Pero ninguna lista ha recibido la atención de los premios del Instituto Clay de Matemáticas anunciados el 24 de mayo del 2000. Como pasa con la lista de Hilbert, contiene problemas de todas las grandes áreas de la matemática. Solo uno de estos se ha resuelto, la conjetura de Poincaré. En los siguientes artículos se pueden encontrar breves introducciones a algunos: pasen y vean.
REFERENCIAS
Boyer, C. B. (1989). A history of mathematics. Nueva York: John Wiley & Sons, Inc.
Dunham, W. (1990). Journey through genius. Nueva York: John Wiley & Sons, Inc.
Hilbert, D. (1902). Mathematical problems. Bulletin of the American Mathematical Society, 8, 437–479. doi: 10.1090/S0002-9904-1902-00923-3
Kline, M. (1972). Mathematical thought from ancient to modern times. Nueva York: Oxford University Press.