|
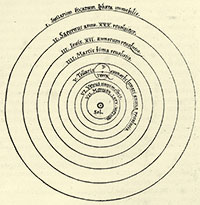
From Heaven to Earth. Astronomy in the Seventeenth and Eighteenth Centuries and its Epistemological Outcome. Actualmente es perfectamente natural pensar que las disciplinas que se estudian en una Facultad de Físicas precisan de la matemática como herramienta indispensable. Sin embargo, la matematización de los fenómenos físicos (movimientos celestes, caída de graves, luz, calor, electricidad, magnetismo, etc.) ha constituido un proceso lento y gradual, que comenzó en Grecia, con la geometrización de los movimientos de los astros. Concretamente en la Academia de Platón se elaboró el primer modelo planetario de carácter geométrico debido a un discípulo de este filósofo, Eudoxo de Cnido (s. iv aC). A dicho modelo siguió otra forma de geometrizar el cielo que, en el siglo ii dC, fue sistematizada y perfeccionada por el alejandrino Claudio Ptolomeo. En ambos casos, conforme a principios platónicos muy consolidados, se partía del supuesto según el cual todos los movimientos celestes son uniformes, circulares y regulares, y tienen lugar alrededor de la Tierra, esto es, son geocéntricos. Este planteamiento fue heredado por la Edad Media (a partir de la recuperación del saber griego a finales del siglo xii) y permanecía vigente en la primera mitad del siglo xvi, época en la cual Nicolás Copérnico (1473-1543) introdujo una reforma que, en principio, podía parecer menor: las órbitas planetarias circulares tenían como centro, no la Tierra, sino el Sol, de modo que el modelo era heliocéntrico. Pero el resto del planteamiento heredado (circularidad y uniformidad de las órbitas) se mantenía. Medio siglo después, ya en el siglo xvii, Johannes Kepler (1571-1630) se contaba entre los escasos autores que, junto con contemporáneos suyos como Galileo Galilei (1564-1642) o René Descartes (1596-1650), aceptaba la reforma heliocéntrica de Copérnico, si bien al principio todavía compartía idénticos presupuestos acerca de la mencionada circularidad y uniformidad de las órbitas celestes. Se comprende así lo radicalmente innovador que fue la formulación de las famosas tres leyes de los movimientos planetarios de Kepler, muy en especial la primera (en la que se sustituían las órbitas circulares por órbitas elípticas) y la segunda (en la que se reemplazaban las velocidades angulares uniformes por velocidades areolares uniformes, lo que de hecho significaba negar la uniformidad de los movimientos planetarios). En ellas se cerraba un capítulo de la historia de la astronomía que se había iniciado en la Academia platónica, al tiempo que comenzaba otro que culminaría en Newton décadas después. Pero siempre manteniéndose la idea de que el cielo podía y debía ser geometrizado. ■ De los movimientos planetarios a las causas: la gravitación universal La astronomía geométrica, desde Platón y Eudoxo hasta Kepler, fue de carácter estrictamente cinemático, de modo que consistía en una pura descripción del desplazamiento espacio-temporal de los cuerpos celestes sin ningún tipo de referencia a la causa que los produce. Esto en modo alguno quiere decir que el tema no hubiera sido planteado, sino que la explicación dominante durante siglos no fue dada por los astrónomos y geómetras sino por los físicos, esto es, por los estudiosos de la physis, herederos de la influyente física cualitativa aristotélica. Y conforme a la tradición aristotélica, vigente todavía en la primera mitad del siglo xvii, el Sol no jugaba papel mecánico alguno, de modo que este astro era fuente de luz y de calor pero no de movimiento. La causa del movimiento de los planetas nada tenía que ver con él. Kepler, no obstante, por primera vez se pregunta en 1619 si tal vez los planetas no permanecerán en reposo a menos que sobre ellos se ejerza una acción motriz, si acaso esa acción no procederá del Sol y si no se debilitará con la distancia puesto que los planetas caminan tanto más lentamente cuanto más alejados están de dicho astro. Con ello Kepler abre un camino a la dinámica celeste (estudio del movimiento a partir de las fuerzas responsables del mismo), que culminará en Newton. Todo el mundo conoce la gran ley de la dinámica de Newton (1642-1727), la ley de gravitación universal formulada en 1687, según la cual la fuerza de la gravedad es directamente proporcional al producto de las masas e inversamente proporcional al cuadrado de su distancia. Pero más allá de la formulación de la ley, cuestión fundamental es la de la naturaleza de la fuerza: por primera vez se afirma que la causa del desplazamiento de los planetas en su órbita es la misma que la que hace caer a los cuerpos sobre la Tierra. Durante siglos se habían tomado como hechos totalmente independientes. No obstante, con Newton la sorpresa será que la gravedad, tradicionalmente considerada como fenómeno exclusivamente terrestre, se aplica también a los fenómenos celestes. En efecto, ahora resulta que si en el cielo se cumplen las tres leyes de Kepler y si en la Tierra rige la ley de caída de los graves (ley del movimiento uniformemente acelerado) publicada por Galileo en 1638, es debido a que sobre todos los cuerpos, tanto celestes como terrestres, actúa la fuerza de la gravedad. La gravitación es universal. Ahora bien, la mecánica newtoniana tenía que afrontar un problema conceptual no desdeñable. Newton había definido la gravedad en términos de fuerza de atracción que opera a distancia. Así, por ejemplo, el Sol atrae a la Tierra (y recíprocamente) sin que entre el Sol y la Tierra medie otra cosa que el espacio vacío. Y la cuestión es cómo puede un cuerpo actuar allí dónde no está, cómo es posible predicar la atracción entre cuerpos inertes, y cómo puede propagarse esa supuesta atracción sin un medio material transmisor. El propio Newton no dejó de considerar que se enfrentaba a un grave problema. El concepto de fuerza de atracción a distancia estaba muy lejos de ser satisfactorio, pero en cambio la ley lo era por completo, puesto que permitía predecir con una exactitud hasta entonces desconocida todo tipo de fenómenos mecánicos en el cielo, en la Tierra y en el mar (mareas). Tras muy diversas vicisitudes, Newton terminó resignándose a no resolver el problema conceptual, pero no sin esgrimir con pasión el mérito de haber hallado lo fundamental: la relación matemática que rige la relación entre los movimientos, ya sean celestes o terrestres, y las causas que los producen (la fuerza de gravitación). En el hallazgo de esa relación residía todo el proyecto teórico que bautizó como mecánica racional, en la cual lo formal, lo preciso, lo cuantitativo, lo predictivo y lo eficaz se iban decantando como valores superiores de explicación. ■ Astronomía mecánica y astronomía observacional El siglo xviii conoció un gran desarrollo, tanto de la astronomía mecánica como de la astronomía de posición. La primera era considerada como una gran parte de la denominada matemática mixta, y su función consistía en realizar los cálculos astronómicos del Sistema Solar. En definitiva se trataba de abordar cuestiones matemático-mecánicas, pero con la importante novedad de traducir la mecánica newtoniana, del lenguaje geométrico en el que había sido escrita, a su versión analítica (de las figuras geométricas a las ecuaciones). Sus principales actores fueron matemáticos franceses, o al menos francófonos, tales como D’Alembert, Euler, Lagrange o Laplace. Como resultado se obtuvo un conocimiento extraordinariamente riguroso y preciso del Sistema Solar, gracias al cual era posible predecir el comportamiento de planetas, satélites y cometas. Simultáneamente, en los grandes observatorios astronómicos fundados en el siglo xvii, como el de París y sobre todo el de Greenwich, se realizaba una paciente y fundamental actividad de observación del Cielo mediante telescopio, fruto de la cual fue la elaboración de excelentes mapas estelares fundamentales, por ejemplo, para la navegación. Pero además la observación telescópica de los cuerpos celestes, inaugurada por Galileo en 1609, introdujo importantes novedades en lo que a los pobladores del Sistema Solar se refiere. Desde la antigüedad griega y hasta la mencionada fecha, el número de planetas había permanecido fijo (Mercurio, Venus, Marte, Júpiter y Saturno, a los cuales con la reforma copernicana se unió la Tierra). Antes de dicha reforma la Luna no era un satélite de la Tierra sino un cuerpo celeste que, como todos los demás (incluido el Sol, que en modo alguno era concebido como una estrella), giraba alrededor de una Tierra inmóvil situada en el centro del mundo. Con Copérnico, todo pasó a desplazarse en torno al Sol, excepto la Luna, que lo hacía alrededor de la Tierra. Por tanto, cuando a principios del siglo xvii Galileo orientó su rudimentario telescopio hacia el Cielo, se tenía conocimiento de seis planetas y un solo satélite (de hecho, a ojo desnudo no se alcanza a ver más). Sin embargo, gracias a la ampliación del tamaño de los objetos, Galileo pudo divisar por primera vez satélites de otros planetas, en concreto cuatro de Júpiter. A partir de entonces la lista no hizo sino aumentar. En 1675 Christiaan Huygens (1629-1695) observó el primer satélite de Saturno, al que siguieron otros cuatro gracias a Giovanni D. Cassini (1625-1712) entre 1671 y 1684. Un siglo más tarde William Herschel (1738-1822), provisto con grandes y potentes telescopios muy diferentes del galileano, daba a conocer dos satélites más de este planeta. Pero lo más extraordinario es que añadió un nuevo planeta a la lista de ellos inamovible durante siglos. Se trata de Urano, localizado por Herschell el 13 de marzo de 1781 (y al principio confundido con un cometa). En 1787 descubrió asimismo dos satélites de dicho planeta. En conjunto puede afirmarse que la combinación de cálculo y observación hicieron de la astronomía la disciplina más prestigiosa de finales del siglo xviii. No es de extrañar que se tratara de conseguir en la Tierra un éxito semejante al obtenido en el estudio del cielo. ■ El programa laplaciano o la visión astronómica de la Naturalesa El gran matemático y astrónomo Pierre Simon Laplace (1749-1827) es quien de manera más explícita apostó por lo que podríamos denominar una «visión astronómica de la naturaleza», esto es, por el empleo del método de la astronomía en la búsqueda de cualquier ley de la naturaleza. En la transición del siglo xviii al xix, al ser la mecánica celeste la ciencia matematizada de la Naturaleza por excelencia, de lo que se trataba era de tender un puente metodológico entre los fenómenos celestes y terrestres, intentando una decidida matematización de los fenómenos relativos a la luz, el calor, la electricidad, el magnetismo o el comportamiento de los fluidos. En este programa sistemático de investigación encabezado por Laplace colaboraron hombres de ciencia de la talla de Poisson, Gay-Lussac, Ampère, Fourier, Coulomb o Lagrange. Nos hallamos en las décadas anteriores a la constitución de la física entendida como conjunto de disciplinas (termodinámica, electromagnetismo, teoría de gases en el marco de la mecánica estadística, etc.). De hecho, durante el siglo xviii, mientras que la mecánica se desarrollaba al abrigo de la matemática aplicada, los temas hoy estudiados bajo el rótulo de física eran desconocidos o se abordaban de manera puramente descriptiva (desde luego ese era el caso del calor, la electricidad o el magnetismo). En cambio, en opinión de Laplace, con respecto a los cuerpos del Sistema Solar había sido posible un planteamiento sistemático, en el que, partiendo de observaciones precisas acumuladas durante siglos, en primer lugar se formularon leyes generales de los movimientos planetarios y en segundo lugar se accedió al supremo y universal principio de gravitación, hasta finalmente descender desde este principio a la explicación de todos los fenómenos celestes (siempre dentro de los límites del Sistema Solar). En definitiva, lo que había permitido la consideración del mundo celeste como sistema era la ley de gravitación universal, y en general la mecánica racional newtoniana que había establecido matemáticamente las relaciones entre movimientos y fuerzas. En ello residía su enorme potencial, pese a los problemas conceptuales anteriormente mencionados. Así, tras el proceso de matematización de los fenómenos celestes, ahora le tocaba el turno a los terrestres, en un ambicioso proyecto cuyas consecuencias se extienden a toda la física posterior. La precisión, el rigor, la capacidad de predicción, la eficacia que proporcionaba el empleo de un lenguaje formal matemático se convirtieron en valores superiores de explicación. Una axiología que estará presente en el debate entre filósofos y científicos durante el romanticismo y en la actualidad. En cualquier caso bien puede afirmarse que desde el cielo se inició una mejor comprensión de la Tierra. Y será precisamente desde la Tierra cuando en el siglo xix se inicie una renovada conquista del cielo, ya no sólo planetario, sino estelar. BIBLIOGRAFIA Ana Rioja Nieto. Profesora titular del Departamento de Filosofía. Universidad Complutense de Madrid. |
«La matematización de los fenómenos físicos ha constituido un proceso lento y gradual,
Anónimo. Johannes Kepler, 1610. Óleo sobre lienzo, 35,5 x 44,5 cm. En 1619 Kepler se plantea por primera vez si los planetas se desplazan a causa de una fuerza común y si ésta procede del Sol, ya que observa que los planetas se desplazan más lentamente cuanto más alejados están del astro.
«durante el siglo xviii los temas hoy estudiados bajo el rótulo de física eran desconocidos o se abordaban de manera puramente descriptiva»
Giusto Suttermans. Galileo Galilei, c. 1640-1650. Óleo sobre lienzo, 59,4 x 80,5 cm. La introducción del telescopio para la observación astronómica por parte de Galileo en 1610 significó una ampliación del universo conocido hasta entonces. Al ampliar el tamaño de los objetos, Galileo vio por primera vez satélites de otros planetas.
William Herschel utilizó grandes y potentes telescopios, como el de la imagen, ya muy diferentes al de Galileo, que le permitieron profundizar en el estudio del Sistema Solar.
El matemático y astrónomo Pierre Laplace apostó por utilizar el método de la astronomía en la búsqueda de cualquier ley de la naturaleza. Se podría decir que Laplace inauguró una «visión astronómica de la naturaleza».
«Durante el siglo XVIII los temas hoy estudiados bajo el rótulo de física eran desconocidos o se abordaban de manera puramente descriptiva»
|