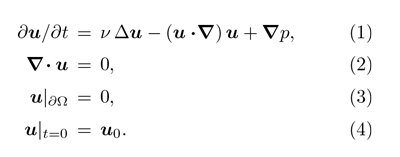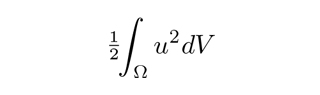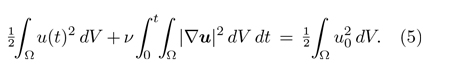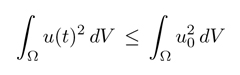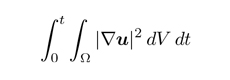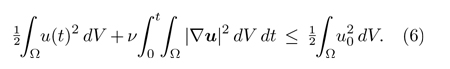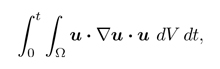Las ecuaciones de Navier-Stokes
¿Impredictibilidad incluso sin mariposas?

Matemáticamente, el movimiento de un fluido se describe mediante las llamadas ecuaciones de Navier-Stokes. En el espíritu de la mecánica newtoniana, estas ecuaciones deberían determinar el movimiento futuro del fluido a partir de su estado inicial. Sin embargo, y a pesar de los notables esfuerzos que se han hecho en esta dirección durante más de un siglo, hasta ahora no se ha conseguido demostrar matemáticamente este determinismo, ni tampoco desmentirlo. En este artículo se da una perspectiva general sobre las ecuaciones de Navier-Stokes, el cuarto de los problemas del milenio.
Palabras clave: ecuaciones de Navier-Stokes, mecánica de fluidos, meteorología, determinismo newtoniano, problemas del milenio.

El huracán Matthew, que se paseó por el mar Caribe del 28 de septiembre al 10 de octubre de 2016, no fue pronosticado hasta cuatro días antes de estas fechas, y entonces solo se le asignó una probabilidad del 70 %. En la imagen, el huracán el 4 de octubre de 2016. / NASA Earth Observatory / Joshua Stevens
Un problema de interés práctico
Uno de los valores más preciados de la ciencia es la capacidad de predecir acontecimientos. En este sentido, destaca particularmente la mecánica celeste, que permite predecir, por ejemplo, que el día 14 de mayo del año 2887 tendrá lugar un eclipse anular de Sol que será visible desde mi ciudad inmediatamente después de la salida del Sol.
En meteorología, donde los pronósticos tienen mucho interés práctico, la situación es bastante diferente. A pesar de los notables progresos que se han hecho, aquí no se pueden hacer predicciones con mucha antelación, incluso sobre fenómenos de gran intensidad y extensión. Así, el huracán Matthew, que se paseó destructivamente por el mar Caribe del 28 de septiembre al 10 de octubre de 2016, no fue pronosticado hasta cuatro días antes de estas fechas, y entonces solo se le asignó una probabilidad del 70 %.
Y no parece que sea cuestión de la precisión y resolución de los datos o de la potencia de cálculo. Estos parámetros no cesan de mejorar sin que ello repercuta muy significativamente en la extensión temporal de los pronósticos meteorológicos. Es natural, pues, preguntarse si tal vez existe algún límite intrínseco en la antelación con la que se pueden hacer predicciones en este campo.
«Uno de los valores más preciados de la ciencia es la capacidad de predecir acontecimientos»
No se trata solo del famoso «efecto mariposa», que depende del hecho de que los datos tengan una precisión limitada. Lo que estamos planteando es la posibilidad de que el futuro sea impredecible ¡incluso suponiendo que los datos tengan una precisión infinita!
Se puede argumentar que los procesos meteorológicos son muy complejos. Ante eso, conviene prescindir de complicaciones no esenciales y considerar un sistema más sencillo, cuanto más mejor, donde continúe teniendo sentido la pregunta que nos estamos haciendo: si existe o no un límite intrínseco en la extensión temporal de las predicciones.
«Es natural preguntarse si tal vez existe algún límite intrínseco en la antelación con la que se pueden hacer predicciones en el campo de la meteorología»
Consideremos, por ejemplo, un recipiente cerrado e inmóvil que está totalmente lleno de agua. Supongamos que justo antes de cerrar el recipiente hemos puesto el agua en movimiento con cierta fuerza. Supongamos, aún más, que justo después de cerrar el recipiente supiésemos exactamente la magnitud y dirección de la velocidad del agua en cada punto. ¿Sería posible, entonces, predecir los valores de estas mismas variables para instantes futuros hasta que el agua esté prácticamente en reposo?

A pesar de los notables progresos que se han alcanzado en meteorología, no se pueden hacer predicciones con mucha antelación, incluso sobre fenómenos de gran intensidad y extensión. Arriba, tornado anticiclónico en Simla, Colorado, en junio de 2015. / James Stuart
Les ecuaciones de movimiento
Las posibilidades de predecir el futuro de un sistema mecánico se basan en las llamadas ecuaciones de movimiento. En el caso de la mecánica celeste se trata de la segunda ley de Newton combinada con la ley de la gravitación universal. Según estas leyes, el movimiento de los astros no puede ser cualquiera, sino que la aceleración de cada astro –la segunda derivada temporal de su posición– queda determinada por las posiciones de todos los otros en relación con él. Tal como mostró Newton, este hecho permite calcular cómo irán variando las velocidades y posiciones de todos los astros, siempre que conozcamos los valores iniciales de estas mismas variables.
La extensión de estas ideas al caso de un fluido no es trivial. De entrada, hay que decidir si modelamos el fluido como un continuo ininterrumpido, o bien lo consideramos compuesto de un gran número de partículas separadas. Aquí nos limitaremos a la primera vía, que es la más clásica y por otro lado es el escenario en el que se sitúa el tema de este artículo.

El cuarto de los problemas del milenio recibe el nombre de los matemáticos Claude-Louis Henri Navier (1785-1836), a la izquierda, y George Gabriel Stokes (1819-1903), a la derecha. Como resultado de sus investigaciones quedó establecido que el movimiento de un fluido viscoso e incompresible en un recipiente cerrado e inmóvil se puede modelar mediante las que hoy conocemos como «ecuaciones de Navier-Stokes». / Mètode
Las ecuaciones de movimiento de un fluido fueron obtenidas por Leonhard Euler a mediados del siglo xviii. En el fondo, no hizo sino aplicar el principio de conservación de la masa y la segunda ley de Newton a una colección bastante rica de partes materiales del fluido. Una parte material la podemos identificar con la región del espacio que ocupa en un determinado instante. Pero al cabo de un momento ocupará otra, que dependerá de cómo se esté moviendo el fluido. Más concretamente, Euler consideró partes materiales infinitesimales: para cada instante de tiempo y alrededor de cada punto, consideraba la materia contenida en un ortoedro de aristas infinitesimales dx, dy, dz. Eso le llevó hacia las ecuaciones del movimiento en forma diferencial.
Las fuerzas que actúan sobre una parte material de fluido se dividen en dos clases: las que actúan a distancia, como la gravedad, y las que actúan por contacto con las partes materiales contiguas, como la presión. Euler consideró tanto la gravedad como la presión, pero no entró en otra fuerza de contacto que es esencial, por ejemplo, para deducir que el agua de nuestro recipiente cerrado tenderá al reposo. Para ello hay que incluir también la viscosidad, que se puede entender como una fricción interna que se opone a las diferencias de velocidad. Las fuerzas de contacto asociadas con la viscosidad no fueron modeladas adecuadamente hasta bien entrado el siglo xix. Ello fue obra más o menos independiente de Claude Navier, Augustin Cauchy, Siméon Poisson, Adhémar Barré de Saint-Venant y George Gabriel Stokes.
Como resultado de sus investigaciones quedó establecido que el movimiento de un fluido viscoso e incompresible en un recipiente cerrado e inmóvil se puede modelar mediante las que hoy conocemos como «ecuaciones de Navier-Stokes». En notación vectorial se pueden escribir así:
En principio hay dos incógnitas, la velocidad u y la presión p, que son funciones de la posición x y del tiempo t. La posición x recorre toda la región Ω ocupada por el fluido. El tiempo t avanza desde 0 hacia +∞. Para ser exactos, todos los términos de la ecuación 1 salvo el último habrían de aparecer multiplicados por la densidad del fluido, pero de ahora en adelante supondremos que esta es la misma en todas partes y que las unidades se han escogido de forma que su valor sea 1. Existe también un parámetro, ν, que varía según el fluido y cuantifica su grado de viscosidad. El resto de la notación es habitual en cálculo vectorial: ∇ = (∂/∂x,∂/∂y,∂/∂z) es el operador gradiente, el cual utilizamos formalmente como un vector que podemos multiplicar escalarmente por otro; en particular, ∇·u es la divergencia del campo vectorial u, y u·∇ es el llamado operador de advección; finalmente, Δ es el operador de Laplace Δ = ∇·∇.
Las ecuaciones 1 y 2 se tienen que cumplir en cualquier punto de la región Ω. En cambio, la ecuación 3 se refiere solo a la superficie ∂ Ω que limita Ω: para un fluido viscoso, la velocidad se debe anular en cualquier punto de esta superficie. En el espíritu de eliminar ciertas complicaciones a que da lugar la ecuación 3, a menudo se considera también el caso en que Ω es todo el espacio, sin ninguna superficie límite. En este caso, se suele añadir, sin embargo, alguna condición asintótica al infinito, o bien simplemente una condición de finitud de la energía (cinética) total
(donde u denota la magnitud del vector u), o tal vez una condición de periodicidad espacial en tres direcciones ortogonales; en lo que sigue sobrentenderemos que hay alguna condición u otra de este tipo, aunque no lo especifiquemos. Finalmente, la ecuación 4 especifica el estado inicial de movimiento del fluido.

A pesar de pertenecer a una familia perseguida por el régimen de Stalin, Olga Ladyzhenskaya (1922-2004) se convirtió en uno de los más destacados miembros de la escuela soviética de ecuaciones en derivadas parciales. Su tema de investigación favorito fue la teoría matemática de los fluidos incompresibles. / Images des Mathématiques
Pues bien, la pregunta que formulábamos más arriba toma ahora la siguiente forma: ¿es cierto que para cada estado inicial u0 hay una sola solución de las ecuaciones de Navier-Stokes, y que esta permanece definida para tiempos arbitrariamente grandes? A continuación examinaremos los estudios que se han hecho para darle respuesta, los cuales han sido obra principalmente de Carl Oseen, Jean Leray y Olga Ladyzhenskaya a lo largo del siglo XX.
Soluciones clásicas
La existencia y unicidad de soluciones de las ecuaciones de Navier-Stokes dado el estado inicial se puede estudiar mediante un procedimiento de aproximaciones sucesivas: partiendo de una primera aproximación, podemos introducirla en el término no lineal de la ecuación 1 –el que contiene (u·∇)u– y tratar de resolver la ecuación resultante para obtener una nueva aproximación; hecho eso, podemos repetir el mismo proceso a partir de esta, y así sucesivamente, con la esperanza de acercarnos cada vez más a la solución exacta. A diferencia de la ecuación 1, la que nos planteamos en cada paso de esta iteración es lineal (no homogénea). Relacionado con eso, su solución se puede expresar mediante una combinación integral de ciertas soluciones especiales que corresponden a impulsos puntuales e instantáneos.
Siguiendo este camino, Oseen y Leray consiguieron tratar, entre otros, el caso en que Ω es todo el espacio, para el cual se pueden calcular explícitamente las soluciones especiales mencionadas. Prescindiendo de ciertos detalles técnicos, los resultados que obtuvieron son los siguientes:
a) Si el tiempo hasta el cual se pide una solución se limita a un valor bastante pequeño, entonces obtenemos una solución y solo una.
b) En general la solución no se puede extender más allá de un cierto tiempo T que puede ser finito o infinito y depende del estado inicial.
c) Si T es finito, entonces la solución desarrolla singularidades cuando t se acerca a T; en otras palabras, existen puntos X de Ω tales que la velocidad toma valores arbitrariamente grandes cuando nos acercamos a (X, T).
De hecho, el método de aproximaciones sucesivas sustituye las ecuaciones diferenciales 1–4 por una ecuación integral. Esta ecuación permite ver que, mientras no aparecen singularidades, las soluciones obtenidas son funciones regulares, es decir, infinitamente diferenciables, y cumplen las ecuaciones diferenciales en el sentido clásico.
De acuerdo con el contrarecíproco de (c), para garantizar que la solución permanece definida para tiempos arbitrariamente grandes basta con obtener una cota superior sobre la magnitud que puede llegar a tener el vector velocidad. Relacionado con eso, no cuesta mucho ver que la energía (cinética) total del fluido disminuye con el tiempo. En efecto, tal como observó Stokes, multiplicando escalarmente la ecuación 1 por u e integrando por partes, se obtiene la llamada «igualdad de la energía»:
Sin embargo, el hecho de que una integral sea finita no excluye la posibilidad de que el integrando se haga infinito en algún punto. En otras palabras, la desigualdad
que se deduce de la ecuación 5 no basta para obtener la globalidad de la solución.
Dicho eso, en el caso bidimensional (Ω ⊆ R2) la acotación sobre
que también se deduce de la ecuación 5 permite llegar a obtener la cota superior mencionada, garantizando así que la solución permanece definida para tiempos arbitrariamente grandes, sea cual sea el estado inicial.
En cambio, en el caso tridimensional, la globalidad temporal de la solución tan solo se ha obtenido en el supuesto de que la energía y velocidades iniciales son lo bastante pequeñas, o que la viscosidad es lo bastante grande.
Singularidades y turbulencia
Es interesante observar que, en la práctica, las dificultades de predicción tienen lugar precisamente en condiciones contrarias a las del resultado que acabamos de comentar; es decir, para velocidades grandes y viscosidades pequeñas. En este sentido es bastante ilustrativo el experimento de Osborne Reynolds, en 1883, sobre la turbulencia, en el que se visualizan las evoluciones espaciotemporales claramente impredecibles que tienen lugar en estas condiciones.
Todo eso lleva a conjeturar que efectivamente las soluciones de las ecuaciones de Navier-Stokes podrían desarrollar singularidades, las cuales estarían relacionadas con las dificultades de predicción detallada de los movimientos turbulentos.
Cuando menos, esta es la opinión que expresaron tanto Oseen como Leray y Ladyzhenskaya. Las citas que siguen se pueden encontrar todas ellas en Mora (2008).
Así, ya en 1910 Oseen se expresaba en los siguientes términos:
Según nuestra teoría, parece, pues, verosímil que puedan nacer irregularidades en el interior de un fluido viscoso e incompresible, incluso en el caso en el que las fuerzas exteriores y el movimiento inicial son completamente regulares.
Y en su libro de 1927 hablaba explícitamente de la posible relación entre singularidades y turbulencia:
Si pueden aparecer singularidades, entonces es obvio que hay que distinguir dos tipos de movimiento de un fluido viscoso, a saber, los movimientos sin singularidades y los movimientos con singularidades. Por otro lado, en hidráulica ya se distinguen dos tipos de movimientos: los movimientos laminares y los movimientos turbulentos. Eso lleva a suponer que los movimientos «laminares» de los experimentos corresponden a los movimientos «regulares» de la teoría, y que los movimientos «turbulentos» de los experimentos corresponden a los movimientos «irregulares» de la teoría. Solo futuras investigaciones permitirán averiguar si esta suposición corresponde o no a la verdad.
Por lo que respecta a Leray, no hay más que decir que adoptó la denominación de «soluciones turbulentas» para referirse a una noción generalizada de solución que, como veremos más abajo, permitiría ir más allá de algunos tipos de singularidades. Además, también se pronunció explícitamente a favor de la conjetura de que las soluciones pueden desarrollar singularidades:
Pero a partir de este hecho no parece para nada posible deducir que el movimiento permanezca por sí mismo regular; yo he indicado incluso una razón que me hace creer en la existencia de movimientos que se convierten en irregulares al cabo de un tiempo finito; desgraciadamente, sin embargo, no he conseguido construir un ejemplo de tal tipo de singularidad.
Finalmente, por lo que respecta a Ladyzhenskaya, podemos citar el siguiente texto, que alude a la falta de unicidad que, según veremos más abajo, podría darse después de las singularidades:
Pero no se puede excluir la posibilidad de que esta regularidad se destruya en algún momento. […] En tales momentos catastróficos la solución se puede ramificar. […] Nosotros pensamos que tal ramificación de la solución es posible en las ecuaciones de Navier-Stokes.
Soluciones débiles globalmente disipativas
ciones de Navier-Stokes desarrollen singularidades, es natural plantearse la siguiente pregunta: ¿se puede dar sentido a las ecuaciones de Navier-Stokes para campos de velocidades que contengan singularidades?
En efecto, la presencia de una singularidad implica que la velocidad no está bien definida en todas partes, y menos aún sus derivadas, de forma que dejan de tener sentido los diversos términos de las ecuaciones diferenciales que se suponía que debían determinar el movimiento futuro del fluido.
En este sentido, Oseen ya observó que la ecuación integral del método de aproximaciones sucesivas puede seguir teniendo sentido en presencia de singularidades. No solamente eso; de hecho, mostró que esta ecuación integral se podía obtener directamente a partir de las ecuaciones que hacen balance de masa y cantidad de movimiento para una parte material finita (no infinitesimal, como había hecho Euler).
Notablemente, uno de los pasos intermedios de esta deducción corresponde a una noción generalizada de solución que después fue adoptada por Leray y que actualmente constituye una herramienta habitual en el estudio de las ecuaciones en derivadas parciales. Estas soluciones en un sentido más general se llaman «soluciones débiles». Así pues, la pregunta que nos planteábamos más arriba tiene una respuesta positiva.
Por otro lado, también es cierto que las ecuaciones de Navier-Stokes significan que las fuerzas de fricción dependen linealmente de las derivadas espaciales de la velocidad, lo cual podría dejar de ser cierto para valores elevados de estas derivadas. Eso da pie a reemplazar las ecuaciones por ciertas variaciones que admiten soluciones globales para cualquier estado inicial, y estudiar el límite de estas soluciones, para un estado inicial dado, cuando nos acercamos cada vez más a las ecuaciones de Navier-Stokes.
Al desarrollar esta idea, Leray no pudo garantizar un límite único para toda la sucesión de soluciones perturbadas, sino solamente la existencia de subsucesiones convergentes en un sentido determinado, con límites que podrían cambiar de una subsucesión a la otra. Eso sí, cada uno de estos límites es una solución débil global de las ecuaciones de Navier-Stokes para el estado inicial dado.
La forma en que Leray había modificado las ecuaciones tenía la particularidad de que las soluciones perturbadas cumplían todas ellas la igualdad de la energía (ecuación 5). Pese a ello, el sentido en que convergen las subsucesiones mencionadas es demasiado débil para garantizar que el límite cumple la misma igualdad. Lo que sí que se puede deducir, sin embargo, es que las soluciones débiles obtenidas cumplen la llamada «desigualdad de la energía», donde el signo «=» de la ecuación 5 es reemplazado por «≤»:
Nótese que esta desigualdad no ha sido en absoluto deducida de que u sea solución en sentido débil. Y es que no existe tal deducción. Cuando menos, el camino que hemos seguido para las soluciones clásicas –los cálculos de Stokes que hemos indicado en el tercer apartado– no es practicable, ya que pasa por la integral
la cual no tiene sentido en las condiciones de poca regularidad que supone la noción de solución débil.
Ante ello, y ante la importancia que tiene la desigualdad de la energía, conviene introducir un nuevo concepto de solución que pida explícitamente el cumplimiento de esta desigualdad además de satisfacer la ecuación en sentido débil. Estas son las que Leray llamaba «soluciones turbulentas». En vez de eso, nosotros las llamaremos «soluciones globalmente disipativas».
Soluciones débiles localmente disipativas
Recuérdese que las soluciones regulares cumplen la ecuación 6 en forma de igualdad. Esta igualdad cuantifica cómo va disminuyendo la energía a causa de la viscosidad. Por tanto, cuando pedimos que una solución débil cumpla la desigualdad 6, lo que estamos diciendo es lo siguiente: si las singularidades conllevan una desviación respecto a la igualdad de la energía, esta desviación debe ir en la dirección de constituir una disminución adicional de la energía.
«La mecánica de fluidos no es tan diferente de la mecánica celeste por lo que respecta al determinismo»
Esta restricción va en la línea del segundo principio de la termodinámica, que en el contexto que nos ocupa se refiere a la disipación de la energía cinética macroscópica por conversión en energía microscópica. Sin embargo, el segundo principio se debe cumplir no solo en todo el fluido en conjunto, sino también en cualquier parte de este.
Eso lleva de forma natural a un concepto más restrictivo de solución que incluye una versión local de la desigualdad de la energía. Estas soluciones, que podemos llamar «soluciones localmente dispativas», fueron introducidas en 1977 por Vladimir Scheffer. Este autor comprobó que las soluciones débiles que da el procedimiento de perturbación de Leray cumplen la condición mencionada, y utilizó este hecho para acotar la dimensión del conjunto de singularidades. Posteriormente, estos resultados han sido mejorados por Luis Caffarelli, Robert Kohn y Louis Nirenberg, entre otros autores.
Conclusión
«Las posibilidades de predecir el futuro de un sistema mecánico se basan en las ecuaciones de movimiento»
Así pues, el problema continúa siendo esencialmente el que planteábamos en el segundo apartado («Las ecuaciones de movimiento»), a saber, si para cada estado inicial existe una sola solución y esta permanece definida para tiempos arbitrariamente grandes. Pero también hemos visto que el concepto de solución admite ciertas variaciones, de forma que ahora conviene considerarlo también como parte de la respuesta.
Hay que decir que el problema que es objeto de premio por parte del Instituto Clay no es exactamente este, sino que se refiere a la conjetura que hemos formulado en el cuarto apartado («Singularidades y turbulencia»): aclarar –mediante una demostración o bien un contraejemplo– si las soluciones regulares permanecen definidas para tiempos arbitrariamente grandes o bien pueden desarrollar singularidades en un tiempo finito.
Un fluido está constituido por un gran número de moléculas que chocan entre ellas con una frecuencia muy grande. En la imagen, humo ascendiendo en medio de una corriente horizontal. / Graham Jeffery
Nótese que un ejemplo de solución que desarrollase singularidades daría respuesta a la pregunta precedente, pero no a la pregunta fundamental del determinismo, ya que en principio aún quedaría abierta la posibilidad de que la solución tan solo admitiese una sola continuación en la clase de soluciones débiles localmente disipativas.
Volviendo a la comparación que hacíamos en la introducción, la verdad es que la mecánica celeste tampoco es completamente determinista en el sentido que estamos considerando: incluso en el caso ideal de cuerpos puntuales, no se pueden descartar las colisiones; y en general las colisiones triples admiten múltiples formas de continuar el movimiento.
Así pues, en el fondo la mecánica de fluidos no es tan diferente de la mecánica celeste por lo que respecta al determinismo. Después de todo, un fluido está constituido por un gran número de moléculas que chocan entre ellas con una frecuencia muy grande.
NOTA: Este artículo es un resumen de «Les equacions de Navier-Stokes. Un repte al determinisme newtonià», de Xavier Mora, publicado en el Butlletí de la Societat Catalana de Matemàtiques en 2008 y al que remitimos para detalles más técnicos y referencias bibliográficas minuciosas. Para los avances más recientes remitimos a On global weak solutions to the Cauchy problem for the Navier-Stokes equations with large L3-initial data (Seregin y Šverák, 2017) y sus referencias.
REFERENCIAS
Mora, X. (2008). Les equacions de Navier-Stokes. Un repte al determinisme newtonià. Butlletí de la Societat Catalana de Matemàtiques, 23, 53–120. doi: 10.2436/20.2002.01.12
Seregin, G., & Šverák, V. (2017). On global weak solutions to the Cauchy problem for the Navier-Stokes equations with large L3-initial data. Nonlinear Analysis, 154, 269–296. doi: 10.1016/j.na.2016.01.018