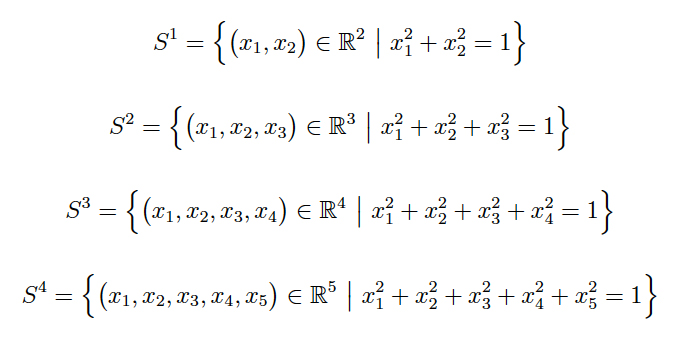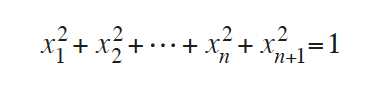La conjetura de Poincaré
Problema resuelto tras un siglo de nuevas ideas y continuo trabajo

La conjetura de Poincaré es un problema topológico, establecido en 1904 por el matemático francés Henri Poincaré, que caracteriza de una manera muy sencilla la esfera tridimensional. Se trata de utilizar únicamente el primer invariante de topología algebraica –el grupo fundamental– también definido y estudiado por Poincaré. La conjetura implica que si un espacio no tiene agujeros esenciales es que se trata de la esfera. Este problema fue resuelto entre 2002 y 2003 por Grigori Perelman, directamente y como consecuencia de su demostración de la conjetura de geometrización de Thurston, que culminaba así el camino marcado por Richard Hamilton.
Palabras clave: topología, esfera, grupo fundamental, geometría riemanniana, flujo de Ricci.
Un trabajo reivindicativo
La conjetura de Poincaré es el único problema del milenio que se ha resuelto. El 18 de marzo de 2010 el Instituto Clay de Matemáticas anunció la concesión del premio de un millón de dólares al matemático ruso Grigori Perelman. Cuatro años antes, Perelman había sido galardonado con una Medalla Fields en el Congreso Internacional de Matemáticos de Madrid de 2006 por sus contribuciones a la geometría y su revolucionaria visión de la estructura analítica y geométrica del flujo de Ricci, pero ni recogió su Medalla Fields ni aceptó el premio del milenio.

El matemático francés Jules Henri Poincaré (1854-1912) propuso en 1904 uno de los problemas más famosos de la historia de las matemáticas, enmarcado en una de sus ramas más abstractas: la topología./ Mètode
Perelman anunció en tres ediciones preliminares publicadas entre 2002 y 2003 en la base de datos de acceso libre arXiv la solución de la conjetura de geometrización de Thurston, que contiene como caso particular la conjetura de Poincaré. Los dos primeros textos, junto con trabajo suyo no publicado o trabajos de otros matemáticos publicados después del 2003, demuestran la conjetura de geometrización. En el tercero, supuestos los resultados esenciales de los otros dos, se da una demostración directa de la conjetura de Poincaré.
La solución de Perelman está basada en ideas de Richard Hamilton usando el flujo de Ricci, que relaciona mediante ecuaciones diferenciales la curvatura con la variación de la métrica. Precisamente Hamilton recibió en 2003 el prestigioso Premio de Investigación Clay por su descubrimiento y desarrollo del flujo de Ricci, una de las más potentes herramientas dentro del análisis geométrico.
Marco inicial de la conjetura: topología
La conjetura de Poincaré se enmarca en una de las ramas más abstractas de las matemáticas, la topología. Su creador, el matemático francés Jules Henri Poincaré, la denominó «analysis situs» y es la parte de las matemáticas que se ocupa de caracterizar algunas propiedades cualitativas de los objetos, aquellas que permanecen en ellos por deformaciones continuas, es decir, suaves, sin roturas, cortes o identificaciones. Es una especie de geometría blanda, no rígida. Esta original idea fue fruto de una mente con una extraordinaria capacidad de abstracción espacial.
Podemos decir que en topología dos objetos –espacios topológicos– son iguales o homeomorfos si uno se obtiene del otro por una deformación continua, es decir, si existe entre ellos una correspondencia biunívoca y bicontinua. Para un topólogo una pelota sigue siendo una esfera a pesar de que esté más o menos hinchada. Tampoco importa su tamaño, es una esfera ya sea de rugby, tenis, tenis de mesa o fútbol. Pero una pelota es topológicamente distinta de un neumático o una tuerca, que tienen un agujero central esencial. Pensemos que el pintor Salvador Dalí actuó como un topólogo cuando pintó sus relojes blandos.
«La conjetura de Poincaré se enmarca en una de las ramas más abstractas de las matemáticas, la topología»
Esta rama de las matemáticas, ampliamente conocida y utilizada por los físicos teóricos, no ha sido justamente valorada por la ciencia en general hasta el descubrimiento reciente de los aislantes topológicos. Se trata de un nuevo tipo de materiales que son aislantes en el interior pero magníficos conductores en el borde. Estas propiedades son debidas a su forma o estructura topológica, que se conserva frente a deformaciones del material. Los físicos teóricos David Thouless, Duncan Haldane y Michael Kosterlitz recibieron el Premio Nobel en 2016 por sus aplicaciones de la topología a la física cuántica de los nuevos materiales. Este premio puso más de actualidad esta disciplina matemática.
Para entender el contexto de la conjetura, analicemos primero algunos conceptos básicos. El espacio es el lugar donde ocurren los fenómenos físicos, donde se mueven los puntos siguiendo las leyes de la física. No todos los espacios permiten los mismos fenómenos, la dimensión representa un papel importante. Intuitivamente la dimensión de un espacio se concibe como el máximo número de direcciones o coordenadas independientes. Así, una curva tiene dimensión 1, una superficie tiene dimensión 2 y nuestro espacio ambiente tiene dimensión i. Podemos imaginar una variedad de dimensión 4 si consideramos como nueva coordenada el tiempo en un espacio físico de dimensión 3.
Los objetos más interesantes de la topología son las variedades. El concepto matemático de variedad de dimensión n (o n-variedad) es la abstracción del espacio de dimensión n. Las variedades son espacios con características similares en todos sus puntos. Es decir, que la situación local en torno a un punto es análoga a la situación local en torno a cualquier otro punto, y análoga a la situación local del clásico espacio físico n-dimensional, es decir, cada punto es el centro de una bola n-dimensional.

En 2016 los físicos teóricos David Thouless, Duncan Haldane y Michael Kosterlitz recibieron el Premio Nobel de Física por sus aplicaciones de la topología a la física cuántica de los nuevos materiales. Cuando se anunciaron los ganadores, el profesor Thors Hans Hansson, que formaba parte del comité del Nobel de Física, usó un rollo de canela (sin agujeros), un bagel (con un agujero) y un pretzel (con dos agujeros) para explicar el concepto de topología. El premio puso de actualidad esta disciplina matemática./ Sergio Segura
Localmente una variedad de dimensión 1 es como un intervalo de la recta; una de dimensión 2, como un disco; una de dimensión 3, como una bola… Si localmente todas las variedades de la misma dimensión son topológicamente iguales, ¿qué podemos decir globalmente? Esta es la pregunta que lleva a plantearse una clasificación global de las variedades. Desearíamos tener una clasificación completa en el sentido de disponer de una lista completa sin repeticiones, es decir, conseguir enumerar una lista de variedades tal que cada variedad es equivalente a una de la lista y solo a una. Analizamos la respuesta por orden creciente de la dimensión.
- Dimensión 1. ¿Cómo es globalmente una variedad de dimensión 1? Entendemos fácilmente que la circunferencia es distinta de la recta real porque, por ejemplo, si nos movemos desde un punto P en una dirección con velocidad constante, en el primer caso llegaremos de nuevo al punto P, pero en el caso de la recta esto no ocurrirá nunca. La circunferencia y la recta son representantes de las dos posibles clases de variedades conexas de dimensión 1. Toda variedad de dimensión 1 está formada por la unión disjunta de líneas cerradas y líneas abiertas, es decir, de circunferencias y rectas.
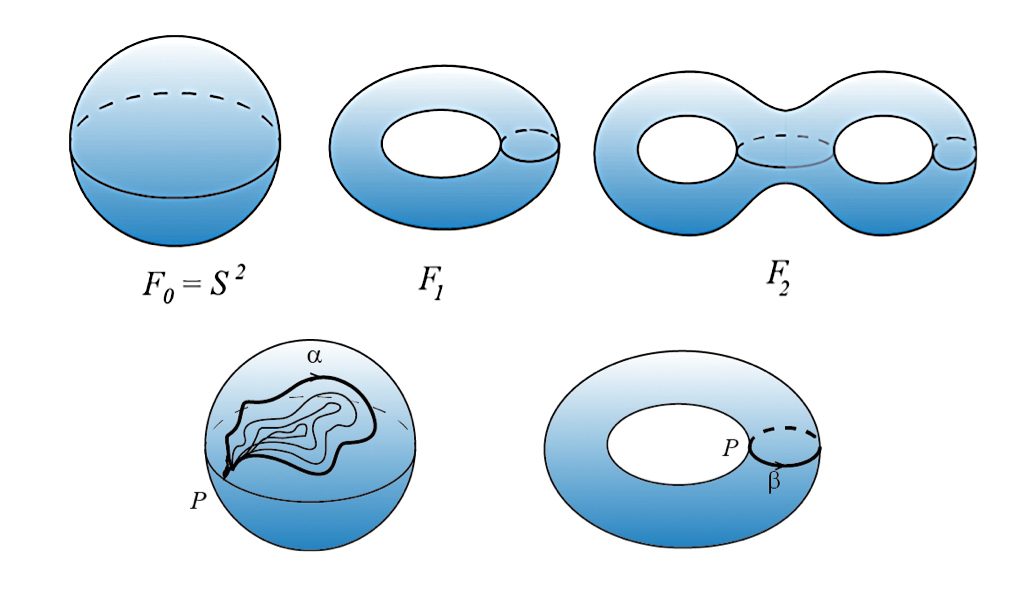
De izquierda a derecha, esfera (superficie orientable cerrada de género
0), toro (género 1) y doble toro (género 2). En topología, los lazos son caminos cerrados que empiezan y terminan en el punto P. En la figura se observan ejemplos de lazos en la esfera (izquierda) y en el toro (derecha).
- Dimensión 2. Una demostración completa de la clasificación de las variedades compactas de dimensión 2 (superficies) es conocida desde el siglo XIX. Una variedad es «compacta» si toda sucesión infinita de puntos contiene una subsucesión convergente. Las superficies compactas se clasifican por su orientabilidad, su género y el número de circunferencias del borde. En las superficies orientables, el género es el número de agujeros esenciales. Así, la esfera sería una superficie orientable cerrada –compacta y sin borde– de género 0; el toro, de género 1 y el doble toro, de género 2.
Para nosotros es fácil entender la diferencia entre dos superficies de distinto género porque las vemos desde fuera gracias a que nuestro campo de visión abarca una dimensión más que nos permite ver globalmente estas superficies. Pero un ser plano, Bidi, viviendo en la superficie, cuyas visuales estén limitadas a su mundo bidimensional, sería incapaz de distinguirlas. Su visión sería necesariamente local y localmente todas las superficies son iguales, igual que un disco. Una demostración rigurosa de la clasificación de superficies puede hacerse usando el grupo fundamental, primer invariante de topología algebraica definido por Poincaré. Dado un punto P sobre una variedad, consideremos caminos sobre la variedad que empiezan y terminan en el punto P. Para nuestros propósitos, identificaremos como iguales dos caminos que se puedan deformar continuamente el uno en el otro, como si de una goma elástica se tratara (se dice entonces que ambos caminos son «homótopos»). Algunos de estos lazos pueden contraerse continuamente hasta quedar reducidos al punto P. Naturalmente, si el lazo rodea un agujero, esto no es posible.
Por ejemplo, en el toro T de la figura 1, un lazo como c se puede contraer a un solo punto, pero los lazos a y b, no. Observemos que los lazos se pueden yuxtaponer poniendo uno a continuación de otro: si P es el punto donde se unen los caminos a y b, podemos definir un camino que empieza en P, sigue por a y cuando vuelve a P sigue por b hasta regresar de nuevo a P. Este lazo es la yuxtaposición de a y b. Nada impide yuxtaponer a y a para dar lugar a un lazo que da dos vueltas, y podemos dar todas las vueltas que deseemos yuxtaponiendo más veces el camino a. De igual manera podemos yuxtaponer b y b para obtener un lazo que rodea dos veces el tubo del toro. No obstante, al yuxtaponer c y c no conseguimos un camino diferente, puesto que el lazo obtenido puede colapsar en un punto. También de la yuxtaposición de b y un lazo como c resulta un lazo que es homótopo a b.
Hay una cuestión importante que aún no hemos tenido en cuenta: un camino se puede recorrer en dos sentidos. Diremos entonces que uno es el inverso del otro. Observemos que si yuxtaponemos un camino y su inverso, conseguimos un lazo que se puede contraer a un punto. En términos matemáticos, hemos obtenido un grupo, al que denotaremos por π1(T, P). Un grupo es una estructura que consta de un conjunto y una operación entre los elementos del conjunto, y esa operación verifica tres propiedades. Nuestro conjunto consiste en las clases de caminos cerrados y la operación es la yuxtaposición. La clase que se puede contraer a un punto es el elemento neutro.
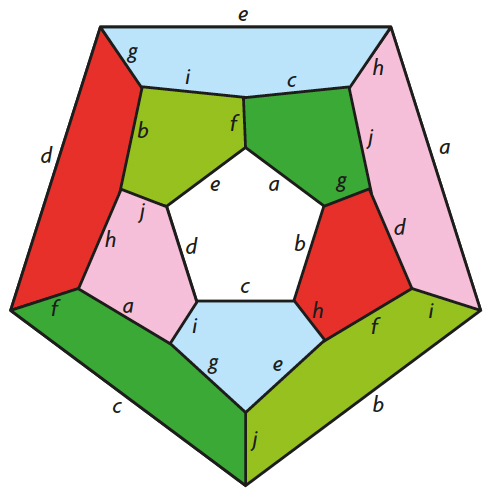
La esfera homológica de Poincaré es el resultado de identificar en
un dodecaedro sólido cada cara con su opuesta por un giro de π/5,
como en esta figura, donde se supone que el plano del dibujo es el
borde del dodecaedro y las caras opuestas tienen el mismo color. / María Teresa Lozano Imízcoz
En general, el grupo fundamental π1(X, P) de un espacio topológico X basado en un punto P del espacio X tiene por elementos las clases de lazos, caminos cerrados que empiezan y terminan en el punto P, y su ley de composición es la yuxtaposición. El elemento neutro es la clase de los caminos α que se deforman continuamente contrayéndose al punto P, siempre sin salirse de la variedad y conservando sus extremos en el punto P. Un grupo se dice que es trivial si se reduce a un único elemento, el neutro. Es fácil observar que todos los caminos cerrados α en la esfera representan el neutro porque siempre se pueden contraer al punto P. Basta imaginar que la imagen del camino es un hilo elástico que se encoge durante la deformación. Luego el grupo fundamental de la esfera es trivial. Pero un camino β en otra superficie Fg distinta de la esfera que rodee un agujero esencial no puede contraerse al punto P sin salirse de la superficie o sin romper el camino.
Cuando el grupo fundamental de una variedad es trivial, se dice que la variedad es «simplemente conexa». Esto es equivalente a decir que todo camino cerrado se contrae continuamente a uno de sus puntos. Con este invariante, el grupo fundamental, tenemos caracterizada la esfera bidimensional: la esfera S2 es la única superficie cerrada simplemente conexa.
- Dimensión 3. Este tema interesa básicamente al científico porque su curiosidad le lleva a querer saber cómo es globalmente el mundo que habitamos, qué forma tiene el universo. Vivimos en un espacio tridimensional, luego nuestra situación para observar globalmente la variedad que habitamos está limitada a una observación local como sucedía al habitante Bidi de la superficie del párrafo anterior. No podemos visualizar globalmente las variedades tridimensionales, así que debemos recurrir al estudio de invariantes para distinguirlas. Los invariantes de variedades son objetos algebraicos (números, polinomios, grupos…) que asociamos a cada variedad de tal manera que en variedades equivalentes un invariante toma el mismo valor.
En el caso de las superficies, la más sencilla es la esfera S2. Si buscamos una representación en coordenadas de la esfera de dimensión n, Sn, la situamos en el espacio euclídeo (n + 1)-dimensional, espacio ordinario de n + 1 dimensiones con la métrica euclídea en la que la distancia más corta entre dos puntos es la línea recta. En este espacio euclídeo la esfera es el espacio topológico de los puntos que equidistan de uno dado, por ejemplo del origen de coordenadas.
Con esta introducción ya podemos entender el enunciado de la conjetura de Poincaré: la esfera S3 es la única variedad de dimensión 3 cerrada simplemente conexa.
Es fácil comprobar que efectivamente el grupo fundamental de la esfera tridimensional es el grupo trivial. El problema es encontrar una variedad tridimensional con grupo fundamental trivial que no sea la esfera (un contraejemplo a la conjetura de Poincaré), o bien demostrar que toda variedad tridimensional con grupo fundamental trivial es topológicamente equivalente a la esfera (confirmar la conjetura de Poincaré).
«En la década de los ochenta irrumpen las técnicas geométricas de la mano del matemático William Thurston, que fue medalla Fields en 1982»
Un enunciado tan sencillo permaneció un siglo sin ser refutado o demostrado. Pero no fue un tiempo perdido, ni mucho menos. El siglo XX fue fructífero en el estudio de técnicas topológicas, geométricas y diferenciales aplicables a 3-variedades que han llevado a un entendimiento profundo de las variedades. Como hemos hecho en superficies, vamos a considerar aquí solo 3-variedades orientables. Si bien el marco inicial de la conjetura de Poincaré era exclusivamente el de la topología, su solución involucra la geometría riemanniana y las ecuaciones diferenciales del flujo de Ricci.
En el siglo XX hubo interesantes descubrimientos en torno a la conjetura de Poincaré. Poincaré definió también el primer grupo de homología, que es el abelianizado del grupo fundamental, es decir el grupo obtenido del grupo fundamental al añadir la conmutatividad de todos sus elementos. El mismo Poincaré, en su Cinquième complément à l’analysis situs (Poincaré, 1904), contesta en negativo a su primera pregunta de aproximación a la conjetura de Poincaré: ¿es suficiente saber que el primer grupo de homología de una 3-variedad es trivial para asegurar que es la 3-esfera? En este artículo obtiene un interesante y bello contraejemplo a esa cuestión: su famosa variedad dodecaedral.
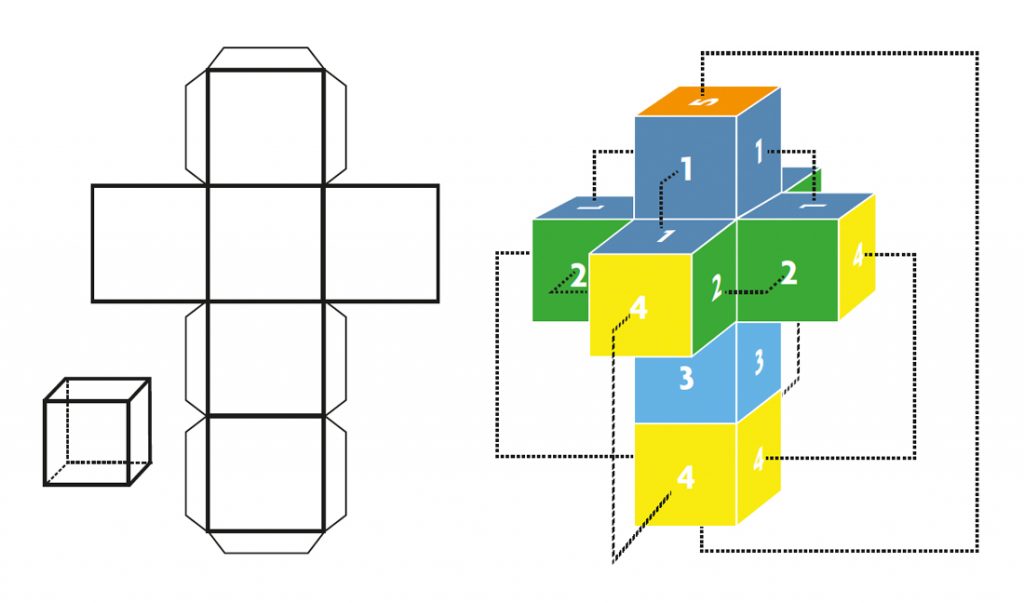
Siempre es difícil imaginar un objeto tridimensional en un espacio de dimensión 4, pero podemos proceder por analogía. De la misma manera
que nos hacemos una idea de un objeto tridimensional como el cubo por medio de su desarrollo plano, se puede intentar imaginar un cubo
4-dimensional a través de su desarrollo espacial. A la izquierda, desarrollo de un cubo en un plano; a la derecha, desarrollo de un hipercubo en
el espacio tridimensional (o más bien de la proyección sobre el plano de su desarrollo espacial). Para obtener la figura tenemos que unir las caras
que tienen igual color, algo imposible de lograr en nuestro espacio de tres dimensiones. / Sergio Segura
Esta variedad, hoy conocida como «esfera homológica de Poincaré» o «espacio dodecaédrico de Poincaré», se puede definir como el conjunto de dodecaedros regulares (o alternativamente icosaedros regulares) inscritos en una esfera bidimensional. Es la variedad resultante de identificar en un dodecaedro sólido cada cara con su opuesta por un giro de π/5. Esta variedad tiene un grupo fundamental finito de 120 elementos, cuyo abelianizado es el grupo trivial, y su recubridor universal es la esfera S3. La variedad dodecaedral se obtiene como cociente de la esfera S3 por la acción de un grupo de isometrías de 120 elementos. Se trata de ver la esfera como el borde del politopo regular de dimensión 4 llamado «la 120 celda». Es decir, ver la esfera S3 teselada por 120 dodecaedros esféricos regulares con ángulos diedrales de 120º, adosados por sus caras (720 pentágonos) donde cada arista es común a tres dodecaedros. En total hay 600 vértices y 1.200 aristas. Estos dodecaedros son intercambiados por un grupo de isometrías. El cociente es la esfera homológica de Poincaré.
El Cinquième complément à l’analysis situs termina con el enunciado correcto de la conjetura de Poincaré establecido como una afirmación. Asegura que la propiedad que caracteriza la esfera tridimensional es la de tener grupo fundamental trivial. La última frase de este escrito es: «Mais cette question nous entraînerait trop loin» (“Pero esta cuestión nos llevaría demasiado lejos”).
Han sido varios los matemáticos que han confesado dedicar parte de sus esfuerzos a demostrarla o a encontrar un contraejemplo, aunque se ha dicho que seguramente todos los topólogos lo hemos intentado en algún momento. La necesidad de hallar nuevos argumentos ha hecho que se hayan encontrado interesantes procedimientos para construir todas las 3-variedades cerradas, en analogía con los procedimientos conocidos para construir todas las superficies cerradas orientables.

Hasta 1980 las técnicas usadas eran topológicas o combinatorias,
pero en la década de los ochenta irrumpen las técnicas geométricas
de la mano del matemático William Thurston. / Bill Wingell, The New York Times
Nuevas ideas: Thurston
Hasta 1980 las técnicas usadas eran topológicas o combinatorias, pero en la década de los ochenta irrumpen las técnicas geométricas de la mano del matemático William Thurston, que fue medalla Fields en 1982. La introducción de una geometría riemanniana en una variedad consiste en definir localmente una métrica de manera coherente que permita medir distancias, ángulos, áreas… La idea intuitiva es endurecer la variedad topológica dándole forma rígida para poder usar las técnicas de la geometría. Si esto se hace en una superficie, es posible hacerlo de manera homogénea de forma que en cada punto de la superficie la curvatura sea la misma. Así la esfera bidimensional tiene curvatura positiva; el toro (o F1), curvatura 0; y las superficies Fg, g > 1, curvatura negativa. Es decir las tres geometrías riemannianas –esférica (de curvatura constante positiva), euclídea (de curvatura cero) e hiperbólica (de curvatura negativa)– son necesarias y suficientes para geometrizar todas la superficies cerradas.
Para llevar esta idea a las 3-variedades es necesario primero partir la variedad en piezas. El proceso tiene cierta analogía con la descomposición de números enteros en factores primos. La idea es dividir la variedad en piezas más simples; estas piezas básicas también se denominan «primas». La división consiste en seccionar la variedad y en pegar esferas obteniendo variedades más simples. Por ejemplo, en superficies, el doble toro se puede seccionar por una circunferencia central, añadir dos discos que cancelan los agujeros creados y obtener dos toros. Las superficies primas orientables son la esfera y el toro. Las variedades primas son las que no se pueden dividir más por este procedimiento. En dimensión 3, una variedad es prima si es S2 × S1, o bien toda esfera encajada bordea una bola.
«Les tres geometries riemannianes –esfèrica, euclidiana i hiperbòlica– són necessàries i suficients per a geometritzar totes la superfícies tancades»
Hellmuth Kneser probó que cada 3-variedad compacta distinta de S3 contiene un número máximo finito de esferas S2 tal que dividen la variedad en diversas piezas de manera que si en cada una de estas piezas se pegan bolas en las esferas de corte se obtienen variedades primas (Kneser, 1929). Más tarde John Milnor probó que esta descomposición en piezas primas es única salvo el orden (Milnor, 1962). Parece razonable entonces restringir el estudio a las variedades primas. Una modificación de los argumentos de Kneser permite cortar una variedad prima a lo largo de un número finito de toros encajados incompresibles y obtener piezas simples que no contienen más toros incompresibles no periféricos. Un toro (F1) es «incompresible» si no se puede comprimir, es decir, si ninguna curva simple cerrada esencial en F1 se deforma continuamente a un punto en la variedad. Esta colección de toros también es única, como asegura el teorema de Jaco-Shalen-Johannson (Jaco y Shalen, 1978; Johannson, 1979).
Una variedad es «geométrica» si es el cociente de una geometría por un grupo discreto de isometrías actuando libre y discontinuamente, y tiene volumen finito. Thurston comprobó que eran necesarias ocho geometrías para geometrizar el interior de las piezas simples y conjeturó que eran suficientes. En concreto estableció la conjetura de geometrización de 3-variedades: cada 3-variedad prima M es geométrica o los interiores de sus piezas simples son variedades geométricas con solo ocho geometrías.
Las ocho geometrías de Thurston –necesarias y suficientes para geometrizar 3-variedades–, perfectamente descritas por Peter Scott (1983) y que agrupamos en tres tipos, son:
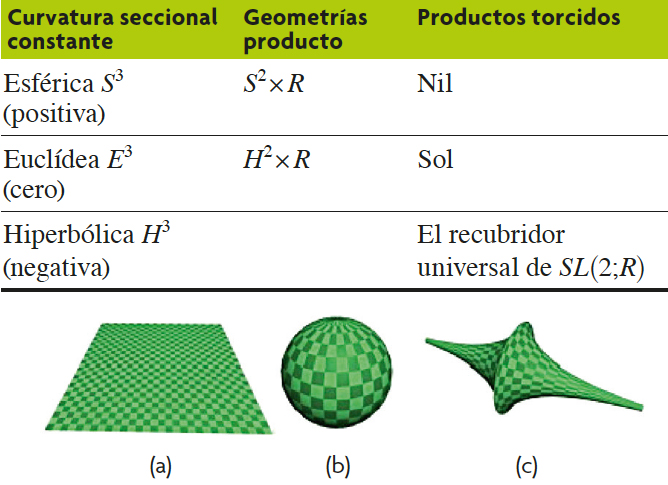
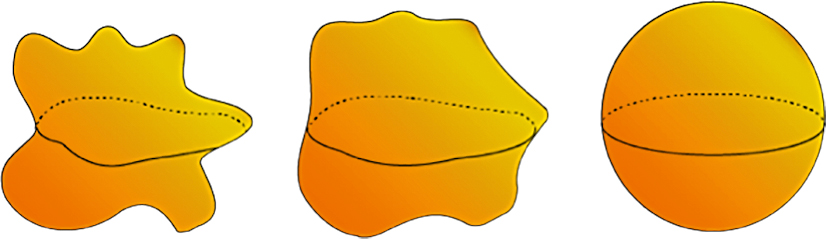
Figura que ilustra las superficies con curvatura constante en el espacio tridimensional. Son el plano (a), que tiene curvatura cero; la esfera (b), que tiene curvatura positiva; y la pseudoesfera (c), que es la superficie generada por una tractriz y tiene curvatura negativa.
Todas las variedades geométricas con geometría distinta de la hiperbólica están clasificadas. Por tanto, tras la demostración de la conjetura de geometrización, solo falta clasificar las variedades hiperbólicas.
La conjetura de Poincaré es un caso especial de la conjetura de geometrización. Obsérvese que, de las ocho geometrías de Thurston, solo es compacta S3, la de curvatura seccional positiva. Si una variedad compacta es simplemente conexa, no contiene toros incompresibles ni esferas esenciales, por tanto la variedad es geométrica y solo puede ser S3.
La descomposición en piezas simples tiene un proceso inverso, una vez que se dota de geometría a las piezas simples. Existen dos maneras de unir 3-variedades geométricas para obtener variedades compuestas. La primera, «suma conexa», consiste en quitar una bola en cada una de ellas y unir los complementos identificando las dos esferas que han quedado como borde. La segunda, que une variedades con borde, trata de identificar sendas componentes del borde por un homeomorfismo. Estas uniones se conocen como «agujeros de gusano» que conectan piezas geométricas. En la suma conexa se trata de un agujero de gusano con sección esférica, y en el segundo caso, de un agujero de gusano que tiene como sección la superficie que sirve de pegado. En teoría, un agujero de gusano en el universo que uniera dos zonas del espacio-tiempo permitiría viajar en el espacio y en el tiempo. Esta idea ha sugerido relatos, novelas y películas donde sus habitantes son capaces de pasar de un mundo a otro a través de estas fronteras, más o menos invisibles, que los conectan.
Thurston demostró su conjetura para una amplia clase de variedades (variedades Haken) que tienen suficiente complejidad para usar sus métodos, métodos que no pueden aplicarse a las variedades simplemente conexas.
El flujo de Ricci: Hamilton
Si se pretende geometrizar una 3-variedad, uno puede empezar definiendo una métrica riemanniana en la variedad y hacer que la métrica cambie con el tiempo tratando de obtener una métrica homogénea en toda la variedad. Si pensamos en superficies, dimensión donde es más fácil entender los conceptos, la idea es pensar, por ejemplo, en una esfera topológica deforme con su métrica correspondiente y conseguir que el paso del tiempo la convierta en una esfera perfecta y redonda. Las técnicas adecuadas para desarrollar estas ideas exigen el uso de ecuaciones diferenciales, inventadas por Isaac Newton para expresar cómo se mueven los cuerpos bajo la influencia de una fuerza externa. En particular, al geómetra le interesa un análogo a la ecuación del calor de Fourier, que es la ecuación diferencial que gobierna el cambio de la temperatura, puesto que con el tiempo consigue una distribución homogénea de la temperatura. Queremos usar una ecuación que relacione el cambio de la geometría con una cualidad geométrica como es la curvatura para conseguir una geometría con una distribución homogénea de la curvatura. Hamilton (1982) definió una ecuación para el flujo de Ricci que contiene por una parte la derivada del tensor métrico y por otra el tensor de Ricci (relacionado con la curvatura): ∂t gij= –2Rij.
La ecuación del flujo de Ricci es la análoga a la ecuación del calor de Fourier pero en un contexto geométrico. Se pretende que homogeneice la curvatura de la misma manera que la del calor homogeneiza la temperatura. La idea es pensar, por ejemplo, en una esfera topológica deforme con su métrica correspondiente y conseguir que el paso del tiempo la convierta en una esfera perfecta y redonda.
Es decir, la ecuación del flujo de Ricci es la análoga a la ecuación del calor de Fourier pero en un contexto geométrico. Se pretende que homogeneice la curvatura de la misma manera que la del calor homogeneiza la temperatura. Si se parte de una variedad con geometría métrica arrugada, se espera que el flujo corrija gradualmente las anomalías y que llegue a una variedad con una geometría regular.
Con estas técnicas Hamilton demostró potentes teoremas, pero encontró obstáculos para demostrar la conjetura de Poincaré. Encontró que se podían producir singularidades en el flujo que no supo resolver y tuvo problemas para analizar la situación en el límite en algunos casos. Las personas interesadas en estudiar el flujo de Ricci pueden consultar Lecture on the Ricci flow, publicado por Peter Topping en 2006 y disponible en línea1.
La solución: Perelman
Fue una sorpresa el anuncio de Perelman dando una solución positiva a la conjetura de geometrización de Thurston en los dos primeros artículos y una demostración directa de la conjetura de Poincaré en el tercer artículo (Perelman, 2002, 2003a, 2003b). Su trabajo se basa en el flujo de Ricci y contiene nuevas ideas para resolver los problemas de singularidades y paso al límite. Entender y validar estos resultados ha sido el trabajo de varios grupos de matemáticos que han ido publicando artículos y libros con exposiciones detalladas del trabajo de Perelman, como Bruce Kleiner y John Lott en Geometry and Topology, publicado en 2008. Aunque su publicación definitiva es posterior a otros artículos, fue el primero que apareció en arXiv, de modo que pudo ser consultado libremente por el resto de equipos. Entre 2006 y 2009 cabe destacar también los trabajos de John Morgan y Gang Tian, Huai-Dong Cao y Xi-Ping Zhu, y Laurent Bessières, Gérard Besson, Michel Boileau, Sylvain Maillot y Joan Porti.
La conjetura de Poincaré en dimensiones superiores
Hasta ahora hemos hablado de S1, S2 y S3, pero nada nos impide aumentar la dimensión y considerar S4, Sn, Sn y así sucesivamente. En general, la n-esfera Sn se define como el conjunto de los vectores
que cumplen
Luego en cualquier dimensión n > 1 cabe plantearse un problema análogo al de la conjetura de Poincaré, si bien ahora la intuición espacial desaparece.
No podemos enunciar en dimensión n la conjetura de Poincaré como que la esfera Sn es la única variedad de dimensión n cerrada y simplemente conexa porque sabemos que existen n-variedades cerradas y simplemente conexas (n > 3) que no son homeomorfas a la esfera de dimensión n (por ejemplo, S2 × S n-2). Por tanto, en dimensión n > 3 hemos de generalizar el grupo fundamental. Una clase de caminos que empiezan y terminan en un punto P es una clase de aplicaciones de S1 en la variedad X que contienen el punto P y puede imaginarse como una goma elástica circular en la variedad y que contiene el punto P. Lo hemos denotado π1(X; P). Con una dimensión más, podemos tomar membranas elásticas esféricas (como globos) que contienen el punto P: son clases de aplicaciones de S2 en X que contienen el punto P y que denotamos π2(X; P). Podemos seguir aumentando la dimensión y definir el grupo de homotopía πi(X; P) como las clases de aplicaciones de Si en X que contienen el punto P.
Dos espacios X, Y son del mismo tipo de homotopía si tienen todos sus respectivos grupos de homotopía isomorfos: πi(X; P) @ πi(Y; Q). El enunciado de la conjetura en dimensión n (CPπin) es: toda n-variedad cerrada del tipo de homotopía de la esfera Sn es equivalente a la esfera Sn.
La conjetura se resolvió primero para dimensión n > 4. A partir de 1960 varios matemáticos probaron por diferentes métodos distintas versiones de la conjetura de Poincaré en dimensión n. En dimensión menor o igual que 3 es indiferente trabajar con variedades topológicas, combinatorias o diferenciables, pero esto no sucede en dimensión superior. La categoría de variedades utilizada y sus correspondientes métodos es lo que distingue las diversas demostraciones.
La prueba en dimensión 4 fue obtenida veinte años más tarde por Michael Freedman. En el mismo artículo clasificó todas las 4-variedades cerradas y simplemente conexas. Freedman recibió también una Medalla Fields en 1986.
En busca de la forma del universo
Hoy disponemos de algunos libros que presentan un desarrollo histórico del tema con contenido accesible a un estudiante universitario. Por ejemplo, The Poincaré conjecture: In search of the shape of the universe (O’Shea, 2007) desarrolla la historia total de la geometría, empezando en la escuela de Pitágoras en el 500 aC, pero sin olvidar a Euclides, la geometría hiperbólica de Gauss, Lobachevsky y Bolyai, las ideas de Riemann y Poincaré. Analiza los avances en el siglo XX y explica con detalle la conjetura de geometrización de Thurston. El subtítulo del libro sirve para estimular la curiosidad del lector y motivar el estudio de variedades tridimensionales.
1 http://homepages.warwick.ac.uk/~maseq/topping_RF_mar06.pdf (Tornar al text)
REFERENCIAS
Hamilton, R. (1982). Three-manifolds with positive Ricci curvature. Journal of Differential Geometry, 17(2), 255–306.
Jaco, W., & Shalen, P. B. (1978). A new decomposition theorem for irreducible sufficiently-large 3-manifolds. En J. Milgram (Ed.), Algebraic and geometric topology (pp. 71–84). Providence: American Mathematical Society. doi: 10.1090/pspum/032.2
Johannson, K. (1979). Homotopy equivalences of 3-manifolds with boundaries. Berlín: Springer-Verlag.
Kneser, H. (1929). Geschlossene Flächen in dreidimesnionalen Mannigfaltigkeiten. Jahresbericht der Deutschen Mathematiker-Vereinigung, 38, 248–260.
Milnor, J. (1962). A unique decomposition theorem for 3-manifolds. American Journal of Mathematics, 84(1), 1–7.
O’Shea, D. (2007). The Poincaré conjecture: In search of the shape of the universe. Nueva York: Walker Publishing Company.
Perelman, G. (2002). The entropy formula for the Ricci flow and its geometric applications. ArXiv. Consultado en https://arxiv.org/abs/math/0211159
Perelman, G. (2003a). Finite extinction time for the solutions to the Ricci flow on certain three-manifolds. ArXiv. Consultado en https://arxiv.org/abs/math/0307245
Perelman, G. (2003b). Ricci flow with surgery on three-manifolds. ArXiv. Consultado en https://arxiv.org/abs/math/0303109
Poincaré, H. (1904). Cinquième complément à l’analysis situs. Rendiconti del Circolo Matematico di Palermo, 18(1), 45–110.
Scott, P. (1983). The geometries of 3-manifolds. Bulletin of the London Mathematical Society, 15(5), 401–487.
AGRADECIMIENTOS
Soporte parcial de MTM2013-45710-c2-1-p, MTM2016-76868-c2-2-p y DGA/Fondo Social Europeo: Grupo Consolidado E15.