Autoorganización fluidodinámica

An almost Exclusively Aesthetic Approach to Self-organising Fluid Dynamics. In this article the author illustrates self-organisation in some fluid dynamic systems, paradigms of complexity. Their complexity can only be approached on an almost exclusively aesthetic level. The evolution of fluid flows, the widely varied instabilities and transitions that are known to exist, turbulence… offer a vast panorama within which, in spite of the progress made, much has yet to be understood.

Al maestro Tomás Marco
en su sexagésimo aniversario

Introducción

Una bifurcación es una reestructuración cualitativa, suave o abrupta, de un sistema dinámico evolutivo que acontece cuando uno de sus parámetros, modificado desde el exterior o quizá espontáneamente, adopta un valor “crítico”, también denominado valor umbral de inestabilidad o bifurcación. Cabe separar las etapas de desarrollo de los momentos de transición, en ocasiones llamados críticos, en los que una inestabilidad puede conducir a nueva forma y/o nueva función. En el primer caso podemos limitarnos, básicamente, a leyes deterministas, aunque continuamente el sistema sufra fluctuaciones que intentan desestabilizarlo. Aquí, pequeñas variaciones en causas originan pequeños efectos y, generalmente, las fluctuaciones decaen. En un punto crítico, los elementos estocásticos (el azar, las fluctuaciones) intentan predominar sobre los deterministas y un cambio suave puede dar un drástico efecto. Determinismo (necesidad) y fluctuaciones (azar) hacen evolucionar el sistema.

«Sistemas tan dispares como el ferromagnetismo, la emisión de luz por un láser o el comportamiento sociológico de animales y humanos son descritos actualmente con una metodología de valor universal»

Las fluctuaciones, espontáneas o forzadas, permiten explorar continuamente nuevas posibilidades, nuevos estados a los que poder llegar y estabilizarse de acuerdo con las ligaduras externas. La “selección” tiene sentido intuitivo si de entre ellos hay alguno de alcance más rápido que los otros, o de estabilidad relativa mayor, o tiene una estructuración o función menos costosa, o ha sido favorecido por alguna causa externa (que puede ser sutil y que es su sesgo o vicio de nacimiento), pero no siempre hablar de selección tiene sentido. Si una fluctuación pasa el nivel umbral de inestabilidad y se establece dominando a toda otra posibilidad o fluctuación del sistema, entonces el estado de partida desaparece por ser ya inestable, y el nuevo estado toma el relevo en la evolución.

Los estados o fases de un sistema, sus “atractores”, puntos fijos, ciclos límite o trayectorias cuasiperiódicas, se caracterizan porque podemos predecir el futuro cualquiera que sea el intervalo de tiempo considerado; generalmente, dos trayectorias inicialmente próximas no se separan apreciablemente a lo largo del tiempo. Dichos atractores eran los únicos conocidos hasta el último tercio del siglo XX, cuando a partir de una observación de B. Saltzman, el meteorólogo E. N. Lorenz, estudiando con computador la evolución, las trayectorias de un modelo muy simplificado de la convección atmosférica, descubrió un ejemplar de atractor aperiódico, caótico (de paso digamos que con dimensión fractal, entre dos y tres). Simultáneamente al descubrimiento “experimental” de Lorenz, y con independencia del mismo, la existencia de atractores caóticos y su estabilidad fueron establecidas por A. N. Kolmogoroff, S. Smale, D. V. Anosov, Ya. G. Sinai, B. Mandelbrot, D. Ruelle, F. Takens y L. P. Shilnikoff, entre otros. Smale propuso una transformación topológica que, como si se amasara pan, permite visualizar lo errático de las órbitas en un atractor aperiódico.

Variedad de fenómenos y universalidad de conceptos y modelos

H. Haken estableció una visión unificada de la muy diversa fenomenología de los sistemas complejos y de su evolución, antes esbozada. Sistemas tan dispares como el ferromagnetismo, la emisión de luz por un láser, la autoorganización fluidodinámica, química o bioquímica (tejidos espaciales, relojes químicos o biológicos, etc.), el comportamiento ecológico e incluso sociológico de animales y humanos, son descritos, actualmente, con una metodología de valor universal. La idea seminal proviene de L. D. Landau, quien imaginó que la muy diversa fenomenología de las transiciones en equilibrio termodinámico podría describirse universalmente si, prescindiendo de los detalles, nos concentramos en la evolución de una, o unas pocas, magnitudes que denominó modos dominantes, parámetros de ordenamiento o de autoorganización. Haken extendió el concepto a los procesos muy alejados del equilibrio, estableciendo que la evolución de esos modos, en el tiempo y en el espacio, dicta el comportamiento sinérgico del sistema, por muy complejo que sea. Nos limitaremos en lo que sigue a ilustrar fenómenos de autoorganización en algunos sistemas fluidodinámicos que ciertamente son paradigmáticos de la complejidad.

Figura 1. Celdas convectivas de Bénard. Cuando se calienta por su base un líquido, por ejemplo aceite de silicona o cualquier otro líquido viscoso, debido a la flotabilidad de Arquímedes o al efecto de la variación de la tensión superficial líquido-aire, o a la combinación simultánea de ambos mecanismos, el sistema evoluciona desde una situación homogénea (sin ordenar) autoorganizándose en celdas de diversas formas, por ejemplo hexagonales. La secuencia permite ver cómo el sesgo debido a la presencia de la pared cilíndrica intenta producir una forma axisimétrica, pero al final la dinámica intrínseca del líquido domina induciendo el panel de abeja.

Formas convectivas estacionarias

La figura 1 muestra el nacimiento de un tejido espacial en celdas convectivas, en un capa o película de líquido calentada por su base y abierta al aire ambiente. La figura 2 (véase también la figura 3) da las líneas de corriente en una celda donde puede observarse cómo las “moléculas” parecen seguirse unas a otras.

Esas celdas, y otras formas convectivas análogas, son consecuencia de uno o dos mecanismos capaces de inducir en una película líquida, en la atmósfera o en el océano, inestabilidad del estado de reposo cuando el sistema está sometido a la influencia externa de un calentamiento, o de adsorción o desorción (incluida la evaporación) de un tensioactivo (moléculas activas en una superficie) si posee una superficie libre o tiene entrefaz con otro líquido.

Fue H. Bénard quien en su tesis doctoral (París, 1900) dejó experimentalmente establecida la autoorganización fluidodinámica en esas celdas convectivas que hoy llevan su nombre. Lord Rayleigh (1916) atribuyó, errónea pero genialmente, la excitación de dichas formas (generalmente hexagonales) a una inestabilidad producida por la flotabilidad de Arquímedes (cuando un fluido se calienta por su base conduce a una situación de cabeza pesada con pies y piernas livianos y, por tanto, mecánicamente inestable). Ese mecanismo favorece la formación de ciertas nubes y, en particular, las calles de nubes cuando hay viento. Es el mecanismo subyacente al modelo atmosférico estudiado por Lorenz.

Lo que ocurre en una película líquida calentada por su base y abierta al aire ambiente, como es el caso de un aceite de silicona en la figura 1 (y en los experimentos de Bénard), es que la tensión superficial líquido-aire se ve afectada por dicho calentamiento. Como dicha tensión, s, depende de la temperatura, si algún punto está más caliente que su entorno cae su valor y entonces se inicia movimiento hacia más frío (efecto explicado por C. Marangoni), pues s es a la superficie (salvo el signo) lo que la presión al volumen del líquido. Al desplazarse líquido en la superficie, el “hueco” es rellenado con líquido que viene de abajo, que está aún más caliente… por lo que la fluctuación inicial tiende a reforzarse. Sin embargo, como un líquido real es viscoso, la viscosidad trata de frenar dicho movimiento. Además, la difusividad calorífica también tiende a eliminarla, aunque muy lentamente (un centímetro en 103s). Es preciso, pues, para que puedan verse las celdas de Bénard, que la diferencia de temperatura entre la base caliente y la superficie superior fría adquiera un valor umbral que supere al frenado viscoso y la termalización (en la práctica unos cuantos grados por milímetro o centímetro según el líquido). La talla horizontal de una celda suele ser del orden del espesor de la película líquida. Idéntico mecanismo ocurre cuando en vez de calentar actúa un tensioactivo. La figura 2 muestra la autoorganización “molecular” en celdas (como las de Bénard) observadas lateralmente.

Diversos aspectos del mismo fenómeno pueden ilustrarse tanto experimental como numéricamente. En particular, la figura 3 muestra cómo se evoluciona desde una situación desordenada (el calor fluye sólo por difusión) a la autoorganización en panel hexagonal (el calor fluye por difusión y convección).

Figura 3. Evolución numérica (obtenida por J. Bragard) desde un estado desordenado, en el que el calor sólo se difunde por la ley de Fourier (véase figura 1), hacia el panel convectivo hexagonal donde la convección se añade a la conducción, debido al efecto de Marangoni por el calentamiento en la base de una película líquida.

Ondas y solitones disipativos

Veamos ahora lo que ocurre si en vez de calentar el líquido por su base, lo enfriamos por ella o bien calentamos el aire sobre la superficie libre. El experimento alternativo consiste en adsorber un vapor liviano (tensioactivo) y esperar hasta que haya sido suficientemente absorbido en el volumen. Tal es el caso de la adsorción de vapor de pentano por una película de tolueno líquido, que es más denso que el líquido pentano y tiene superior tensión superficial con el aire.

Si, de nuevo, imaginamos un punto caliente, como al desplazarse arrastra desde el volumen líquido más frío o más denso, esto hace que la inicial fluctuación de movimiento convectivo tienda a desaparecer; es el proceso ondulatorio o de sobreestabilidad, como si de un péndulo se tratase, que conduce a oscilaciones (ciclos límite), posible formación de ondas superficiales y, con el tiempo, internas, ya que la película líquida, por calentarse en la cabeza o absorber un vapor liviano, se estratifica establemente. En superficie, las ondas se denominan capilares (capilaro-gravitatorias en presencia de gravedad) o dilatantes (debido a la aparente compresión-expansión que se observa). En el volumen, en la atmósfera y en el océano, se las denomina ondas (internas) de Brunt-Väisälä, en honor de los científicos que, pioneramente, las describieron.

Figura 4. Trenes de ondas inducidos en una película líquida calentada por el aire: a) vasija cilíndrica circular; b) vasija anular cilíndrica circular. La visualización es por ombroscopía enviando luz de abajo arriba. El sentido de giro a izquierda o derecha es arbitrario y, en principio, equiprobable.

Las figuras 4 y 5 ilustran fenómenos ondulatorios observados en el laboratorio (cinemáticamente) idénticos a ondas en la naturaleza, en canales de agua, descritas a mediados del siglo XIX por J. S. Russell y luego por H. Bazin, y, poco más tarde, por E. Mach y colaboradores, en el laboratorio con choques gaseosos (así como en resaltos hidráulicos por diversos otros autores). Esos fenómenos, parcial pero clarividentemente estudiados por J. Boussinesq, Lord Rayleigh, D. Korteweg y G. de Vries, a finales del siglo XIX, fueron luego redescubiertos, por N. Zabusky y M. Krustal (1965), integrando numéricamente ecuaciones de ondas extraídas mediante apropiadas simplificaciones de las ecuaciones fluidodinámicas. Dichos autores introdujeron el concepto de solitón en fluidos ideales, sin viscosidad, pues tanto en colisiones frontales o de ángulo arbitrario, como en reflexiones en paredes aisladas, dichas ondas (onda solitaria de Russell, por ejemplo) se comportan (clásicamente, en imagen inversa de la cuántica) más como partículas (electrón, protón, etc.) que como ondas. El concepto de solitón pronto adquirió universalidad y abrió un campo de la matemática aplicada. Las figuras 4 y 5 muestran solitones disipativos. Ondas solitarias, solitones y resaltos (solitónicos) aparecen en diversas situaciones atmosféricas, en ríos (de varios metros de altura: mascaret del río Sena o bore del río Severn) y en estrechos (como en la pycnoclina del estrecho de Gibraltar donde pueden alcanzar hasta cien metros de amplitud aunque sean apenas perceptibles en la superficie del mar) o en el océano (tsunami es una ola gigantesca en un puerto que ocurre como etapa final de una onda solitaria que ha recorrido de tres a cuatro mil kilómetros a unos ochocientos kilómetros por hora, por ejemplo de Alaska a Hawai). El impulso nervioso, potencial de acción o espiga neuronal es un solitón disipativo que puede viajar en axones como el del calamar a unos cuatrocientos kilómetros por hora, prácticamente sin deformarse.

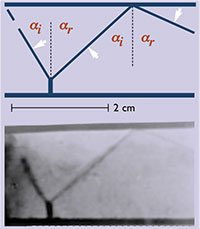
Figura 5. Doble reflexión normal (αi≈αr) y anómala, típicamente solitónica, con brazo de Russell-Mach. Visualización por ombroscopía.

Perspectiva

Tras comentar muy someramente la evolución de los sistemas dinámicos complejos (que aunque no lo hemos dicho, suelen estar regidos por leyes alineales, bucles de realimentación positiva o negativa, retardos en la transmisión de señales, etc.) hemos descrito algunos casos de autoorganización fluidodinámica regida por las ecuaciones de evolución de Navier-Stokes, Fourier y Fick con sus correspondientes condiciones de contorno (e iniciales según los casos) y ecuaciones de estado o constitutivas (de volumen o de superficie). De su complejidad sólo hemos dado una aproximación casi exclusivamente estética, arrimando el ascua a nuestra “sardina”. La evolución de las corrientes fluidas, las muy diversas inestabilidades y transiciones que entre ellas se conocen, la turbulencia apenas disipativa (O. Reynolds, Kolmogoroff), la turbulencia interfacial muy disipativa… ofrecen un vasto panorama del que, aun habiendo mucho entendido, quedan cuestiones básicas por entender. Algunas parecen imposibles de aprehender con capacidad predictiva, tal y como ocurre con la atmósfera si pensamos en el tiempo más allá de unos pocos días.