¿Qué entendemos por diversidad?

El concepto de diversidad biológica ha evolucionado desde el mero recuento de especies a cálculos más sofisticados que tienen en cuenta las abundancias relativas e incluso el tiempo de divergencia evolutiva entre especies. En el curso de esta evolución, las formas de medir la diversidad con frecuencia se han tomado prestadas de otras disciplinas. El razonamiento evolutivo sobre la diversidad suele asumir implícitamente que los cálculos de diversidad responden a ciertas propiedades matemáticas, pero la mayoría de cálculos tradicionales que realizaban los biólogos no cumplían estas propiedades, una situación que a menudo conducía a inferencias inválidas en términos matemáticos y biológicos. Ahora los biólogos suelen transformar los cálculos tradicionales en el «número efectivo de especies», cuya base matemática sí que se adapta a la mayoría de reglas de inferencia que aplican los biólogos. El número efectivo de especies, por lo tanto, parece reflejar la mayoría (no todo) de lo que los biólogos entienden por diversidad.

Palabras clave: diversidad, número efectivo de especies, entropía de Shannon, riqueza de especies.

«A pesar de su importancia, en biología no existe un consenso acerca de lo que significa en realidad la diversidad»

Diversidad es a la vez una palabra de moda y un concepto científico preciso que podemos encontrar en muchas disciplinas. Es uno de los conceptos fundamentales de la biología, particularmente de las subdisciplinas de la ecología, la teoría evolutiva y la genética, pero el mismo concepto –o un análogo cercano– representa un papel importante en la economía, la teoría de la información y la física, entre otros campos. No obstante, a pesar de su importancia, en biología no existe un consenso acerca de lo que significa en realidad o cómo deberíamos cuantificarla. Este tipo de problema siempre es peliagudo para una ciencia joven. Podríamos lograr cierta precisión en su significado simplemente definiendo la diversidad de determinada manera, pero eso es una solución simplista; nada nos garantiza que la diversidad, definida en dichos términos, conecte de forma significativa con futuras teorías. En lugar de establecer una definición forzada de diversidad, la biología ha evolucionado gradualmente hacia un concepto de diversidad que cada vez responde a más requisitos teóricos y prácticos nuevos.

«En la práctica, contar con precisión el número de especies presentes en comunidades ricas resulta casi imposible»

Primeros cálculos de la biodiversidad

Cuando los biólogos empezaron a hablar de diversidad solo se referían al número de especies en una comunidad, lo que se conoce como «riqueza de especies». A primera vista, este concepto de diversidad parece ser sencillo de interpretar, y sin duda refleja una cualidad importante de un ecosistema. En la práctica, sin embargo, contar con precisión el número de especies presentes en comunidades ricas, donde la mayoría de especies suelen ser raras, resulta casi imposible. Por ejemplo, Phil DeVries, Tom Walla y Harold Greeney recopilaron mariposas durante diez años en una única localización de la selva amazónica (DeVries y Walla, 2001). Y tras esos diez años de intensa recolección seguían añadiendo especies que nunca antes habían recogido. Esto es típico de los ecosistemas tropicales. En lugares como esos, el recuento de especies depende en gran medida del trabajo de muestreo y de la distribución de abundancia de sus especies. Utilizando herramientas estadísticas basadas en los decodificadores que Alan Turing creó para los británicos durante la Segunda Guerra Mundial, Anne Chao desarrolló un estimador del límite inferior del número de especies de una comunidad (Chao, 1984), pero resulta imposible estimar sin sesgos el número real de especies.

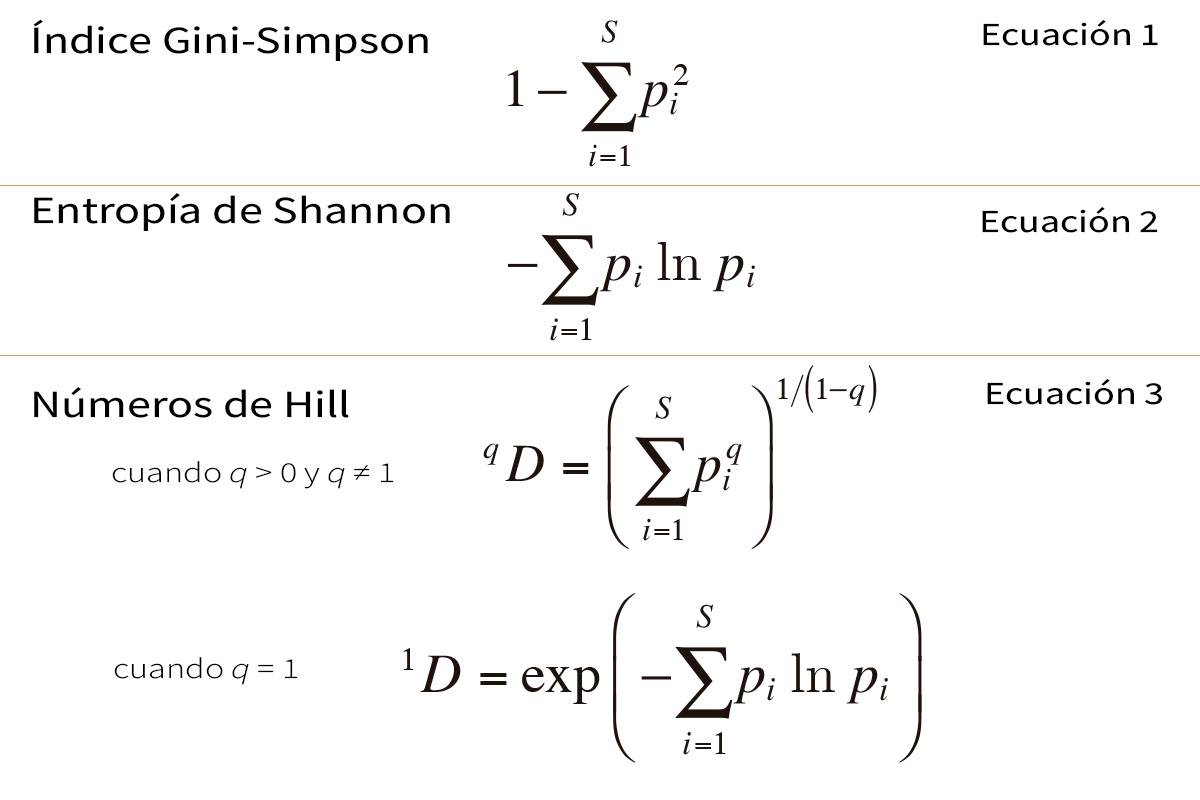
Tabla 1. Las expresiones matemáticas más importantes utilizadas para el cálculo de la diversidad ecológica. S = número de especies; pi = abundancia relativa de la especie i (el número de individuos de la especie i en la comunidad dividido por el número total de individuos de todas las especies, S); q es un parámetro que determina la sensibilidad de la fórmula a las abundancias relativas de las especies.

A pesar de la dificultad de estimación, la riqueza de especies sigue siendo un parámetro de la comunidad biológica importante para muchos propósitos teóricos y prácticos. Por ejemplo, es muy útil para priorizar áreas de conservación. Sin embargo, para muchas aplicaciones el mero recuento de especies no es suficiente. Un robledal con algunos pinos es muy diferente de un pinar con algunos robles. En muchos aspectos ecológicos, una comunidad de mariposas con diez especies que incluya una especie abundante y nueve extremadamente raras se parece más a una comunidad de mariposas con una única especie que a una con diez especies igual de comunes. La forma en la que se distribuyen los individuos de las especies es importante. Un recuento que solo tenga en cuenta la presencia o ausencia de especies no refleja esta diferencia. Los biólogos necesitaban expandir el concepto de diversidad para tener en cuenta la abundancia siempre que fuera necesario. Para un número determinado de especies, la mayor diversidad posible se daría cuando todas las especies son igual de comunes, y el mínimo posible cuando todas las especies menos una son extremadamente raras. En ese caso, la diversidad seguiría disminuyendo según se fueran extinguiendo especies.

Los cálculos de este tipo son importantes en muchas disciplinas que se ocupan de sistemas complejos. Son especialmente prominentes en economía, donde se utilizan (estos u otros cálculos inversos o complementarios) para calcular cosas como la concentración de la riqueza entre individuos o la concentración de capacidad industrial entre corporaciones. Ya hace tiempo que los economistas formalizaron las condiciones necesarias para que disminuya la concentración (y aumente su inverso, la diversidad). La condición principal se conoce como «principio de transferencias Pigou-Dalton» (Jost, 2010). Expresado en términos biológicos, para un número fijo de especies y un número fijo de individuos, la diversidad debería aumentar cuando se transfiere abundancia desde una especie a otra más rara. La diversidad también aumentaría cuando se añade una especie extremadamente rara.

Muchas propiedades de un ecosistema importantes en términos biológicos obedecen al principio de transferencia. Por ejemplo, imaginemos un ecosistema con un número determinado de especies en el que cada individuo deambula al azar y ocasionalmente se encuentra con otro individuo. Cuando dos individuos se encuentran, se puede calcular la probabilidad de que los dos pertenezcan a especies distintas. Esto se conoce habitualmente como índice Gini-Simpson (Ecuación 1 de la Tabla 1), y en el pasado se entendía frecuentemente como un equivalente de la diversidad. La probabilidad de un encuentro entre especies es mínimo cuando todas las especies menos una son extremadamente raras. Al transferir abundancia desde las especies más comunes a las más raras, la probabilidad aumenta hasta que alcanza un máximo cuando todas las especies son igual de comunes. Por lo tanto, la «probabilidad de un encuentro entre especies» obedece al principio de transferencia y puede servir como medida de la complejidad compositiva de un ecosistema. Otra propiedad de un ecosistema de este tipo es la incertidumbre acerca de la especie de un individuo de la comunidad seleccionado al azar. Esta incertidumbre se puede calcular a partir de las abundancias relativas de cada especie mediante la teoría de la información (Shannon, 1948), y es simplemente la entropía de Shannon (Ecuación 2 de la Tabla 1). Los biólogos suelen llamarlo índice de Shannon-Weiner o índice de Shannon-Weaver. Para un número dado de especies, este índice alcanza el mínimo cuando todas las especies menos una son extremadamente raras, y el máximo cuando todas las especies son igual de comunes. En el pasado, esta medida de la complejidad compositiva también se equiparó con la diversidad.

Interpretar los cálculos de diversidad

Los tres cálculos mencionados hasta ahora –la riqueza de especies, la entropía de Shannon y el índice Gini-Simpson– se han utilizado para cuantificar la diversidad, a menudo al mismo tiempo. Sin embargo, cada uno de ellos se expresa en unidades distintas y presenta comportamientos matemáticos diferentes. La riqueza de especies es una medida discreta con valores enteros, expresada en «especies», mientras que la entropía de Shannon es una función continua sin límite superior, expresada en «bits», y el índice Gini-Simpson es una probabilidad que nunca puede exceder la unidad. Aunque sin duda estos cálculos están relacionados con el concepto biológico de diversidad, tienen propiedades matemáticas tan diferentes que sus valores no se pueden comparar directamente y, en general, la lógica que funciona con uno de ellos es inválida cuando se aplica a los otros dos. Este caos parecía impedir que los expertos lograran un concepto de diversidad razonablemente preciso pero también general y provechoso.

«Un robledal con algunos pinos es muy diferente de un pinar con algunos robles. La forma en la que se distribuyen los individuos de las especies es importante»

No obstante, los biólogos seguían aplicando razonamientos similares a los tres cálculos, como si tuvieran un único concepto de diversidad en mente. Por ejemplo, habitualmente se analizaba el cambio porcentual de cada uno de estos cálculos después de un impacto humano o natural. Esto era problemático porque los biólogos comparaban porcentajes o proporciones con cálculos claramente no lineales (Moreno, Barragán, Pineda y Pavón, 2011). Este método para juzgar la magnitud de un impacto podía ofrecer resultados engañosos cuando se aplicaba a la entropía de Shannon, una medida logarítmica. Era todavía más engañoso cuando se aplicaba al índice Gini-Simpson. Como dicho índice no puede exceder la unidad, todas las comunidades con alta diversidad tienen valores similares, muy cercanos a la unidad. Un cambio biológico enorme en una comunidad (por ejemplo, la extinción de un 90 % de las especies) podría provocar un cambio inferior a un 1 % en el valor de este índice.

Este problema se hizo más obvio cuando los biólogos comenzaron a utilizar estos cálculos de la diversidad para evaluar la similitud compositiva entre comunidades. Los biólogos notaron que había una conexión muy profunda entre similitud compositiva y diversidad. Si se agrupan en la misma proporción dos comunidades que tienen las mismas especies con la misma abundancia relativa, la diversidad de la comunidad agregada será la misma que la de las comunidades originales. Por otro lado, si la composición de las dos comunidades era muy diferente, entonces la diversidad de la comunidad agregada será mucho mayor que la media de diversidad de las dos comunidades individuales. Comparando la diversidad media de cada comunidad con la diversidad de la comunidad agregada, se podría cuantificar el grado relativo de similitud compositiva entre ellas. Normalmente se comparaba dividiendo las dos diversidades (Lande, 1996). Esto era útil cuando la medida de la diversidad utilizada era la riqueza de especies, pero para la entropía de Shannon y el índice Gini-Simpson, presentaba el mismo problema mencionado en el párrafo anterior: estos cálculos son no lineales, por lo que comparar las proporciones resulta engañoso. Por ejemplo, el índice Gini-Simpson no puede exceder de 1,00, por lo que, cuando los índices Gini-Simpson de las comunidades individuales se acercan a la unidad, agregarlos no hace que el índice aumente mucho, incluso cuando las comunidades son completamente diferentes (sin especies en común). Al dividir estas dos diversidades necesariamente obtenemos un número cercano a la unidad, lo que en teoría apunta a un alto nivel de similitud composicional, sin importar si las comunidades son casi idénticas o completamente distintas (Jost, 2006, 2007; Jost et al., 2010).

La dificultad de interpretar este y otros resultados del índice Gini-Simpson y la entropía de Shannon llevó a algunos biólogos a dudar de la utilidad de estos cálculos en biología. El problema, sin embargo, no eran los cálculos sino la insistencia de los biólogos en aplicar las mismas reglas de inferencia a todos ellos, como si todos tuvieran las mismas propiedades matemáticas que la riqueza de especies.

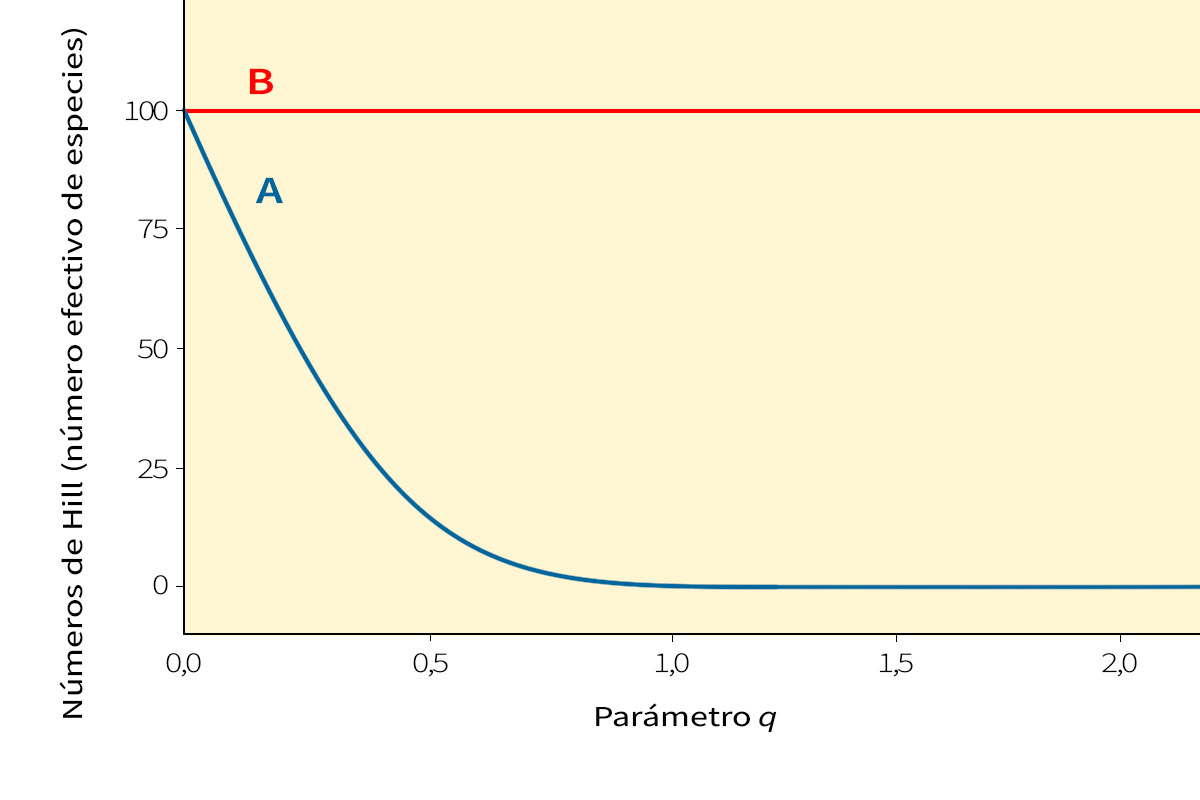
Figura 1. Perfiles de diversidad de dos comunidades con el mismo número de especies (s=100) e individuos (n=1.000), pero con diferente equitatividad. En el perfil A, hay algunas pocas especies que son muy dominantes, mientras que otras son poco abundantes. En el perfil B, todas las especies tienen un número similar de individuos; es decir, hay mayor equitatividad. Los números de Hill (el número efectivo de especies) hacen de fórmula maestra que permite expresar de manera sencilla este número efectivo de especies frente al parámetro q, que determina la sensibilidad del cálculo a la abundancia relativa de especies. Esto nos permite comparar, también gráficamente, diversos perfiles de diversidad como A y B. Ambas comunidades tienen el mismo número de especies, y por tanto la misma diversidad de orden q=0, pero el reparto de los individuos entre las especies es diferente: un desequilibrio mayor (menor equitatividad) se traduce en una menor diversidad de orden 1 y 2 para la comunidad A.

Hacia una fórmula maestra

Un paso clave fue el descubrimiento –realizado independientemente a final del siglo xx por científicos de campos tan diferentes como la ecología, la economía, la teoría de la información y la física– de que estos tres cálculos de la «diversidad» aparentemente no relacionados (o sus transformaciones simples) podían, de hecho, estar generados por una única fórmula maestra. Se descubrieron varias fórmulas maestras, diferentes en cada disciplina, pero solo había pequeñas transformaciones entre unas y otras, por lo que expresaban esencialmente lo mismo. La mayoría se interpretaron como generalizaciones de la entropía de Shannon. Una de las más conocidas de estas fórmulas maestras generó la familia de entropías de Rényi (Rényi, 1961), y otra muy popular dio lugar a las entropías de Tsallis (o HCDT)¹ (Tsallis, 1988). Estas fórmulas maestras pueden generar cada uno de los tres cálculos de «diversidad» (o transformaciones simples de los mismos) variando un parámetro q que controla la sensibilidad del cálculo a las abundancias relativas de las especies. Cuando q = 0, cada una de estas fórmulas maestras proporciona la riqueza de especies, o una transformación simple de esta; cuando q = 1, las fórmulas maestras no están definidas, pero en el límite cercano a 1 proporcionan la entropía de Shannon, o una transformación simple de esta; y cuando q = 2, las fórmulas maestras proporcionan el índice Gini-Simpson, o una transformación simple de este. Esto representaba una unificación interesante e importante de lo que anteriormente parecía un batiburrillo de cálculos sin relación entre ellos. Era la primera señal de que podía existir una «matemática de la diversidad» rica y profunda para poner orden en la disciplina.

Estas fórmulas maestras no se limitan a los valores 0, 1 o 2 para el parámetro q. Se podría usar cualquier valor de q ≥ 0, y al hacer la gráfica de la fórmula maestra con q, se podría crear una curva suave llamada «espectro de entropía (de Rényi o de Tsallis)» de la comunidad. Estas curvas nos ofrecen una forma alternativa de expresar la información contenida en la distribución de abundancias por especie en una comunidad. Si comparamos dos comunidades y observamos qué perfil queda por encima, no hay duda de cuál es más diversa. Si los perfiles se cruzan, el orden de diversidad es ambiguo y depende de la ponderación de las abundancias relativas de especies.

El siguiente gran paso fue el descubrimiento por parte del ecólogo Mark Hill y los economistas Hannah y Kay de que las fórmulas maestras se podían transformar para generar un grupo de cálculos (Ecuación 3 de la Tabla 1) con la misma métrica sencilla de la riqueza de especies, en lugar de entropías no lineales (Hannah y Kay, 1977; Hill, 1973). Los cálculos generados por la nueva fórmula maestra obedecen a un principio que ya era clave en la economía moderna, y que estaba implícito en muchos de los razonamientos de los biólogos con respecto a la diversidad. En economía se conocía este principio como «principio de replicación»: si agregamos una cantidad N de comunidades igualmente diversas y de igual tamaño pero que no comparten especies, la diversidad de la comunidad agregada debería ser N veces la diversidad de una sola de las comunidades. Los cálculos que obedecen a este principio son lineales con respecto al agregado. ¡He aquí la solución a la mala costumbre de comparar porcentajes con la entropía de Shannon o el índice Gini-Simpson! Ahora estos dos cálculos y otros relacionados para diferentes valores del parámetro q se podían transformar en cálculos que ofrecieran los resultados correctos al comparar proporciones y porcentajes. Por fin conseguimos cálculos de la diversidad que respaldaban las reglas de inferencia que los biólogos habían utilizado previamente en cálculos no lineales inadecuados.

«La riqueza de especies sigue siendo un parámetro de la comunidad biológica importante para muchos propósitos teóricos y prácticos»

Estos nuevos cálculos de la diversidad se expresan en unidades de «número efectivo de especies», que se entienden mejor con un ejemplo. Supongamos que la distribución de abundancia de una especie en una comunidad tiene una entropía de Shannon de 2,77 (utilizando logaritmos en base e). Podríamos valorar la magnitud de esa cifra, 2,77, construyendo una comunidad de referencia con la misma entropía pero que incluyera solo un número X de especies igual de comunes. Descubrir el valor de X es una cuestión de álgebra, y en este caso el resultado es X = 16 especies igual de comunes; una comunidad con 16 especies igual de comunes tiene la misma entropía que la comunidad real, 2,77. Por lo tanto el «número efectivo de especies» para una entropía de Shannon de 2,77 corresponde a 16. Si en este ejemplo usamos variables en lugar de números concretos, podemos derivar una fórmula general para convertir la entropía de Shannon en el número efectivo de especies; la fórmula de conversión es simplemente exp(H), donde H es la entropía de Shannon utilizando logaritmos naturales.

Podemos repetir el proceso con una segunda comunidad cuya entropía es 3,46. A primera vista no parece muy diferente de la entropía de la primera comunidad, 2,77. Sin embargo, hacen falta 32 especies igual de comunes para alcanzar una entropía de 3,46. En lo que respecta a la entropía de Shannon, la diferencia entre la primera comunidad y la segunda es igual que la diferencia en entropía entre una comunidad de 16 especies igual de comunes y una de 32. Esto demuestra lo engañosos que pueden resultar los valores de la entropía de Shannon para evaluar los cambios en un ecosistema. Cuando convertimos las entropías en el número efectivo de especies, conseguimos un sentido más claro de su significado. Además, el «número efectivo de especies» es independiente de la base utilizada para calcular el logaritmo en la entropía.

Recientemente se descubrió la radiación evolutiva local de nuevas especies de orquídeas del género Teagueia en el este de Ecuador. Este es un ejemplo de gran diversidad de especies con poca diversidad filogenética. / © Lou Jost/EcoMinga

Podemos utilizar el mismo método para encontrar el número efectivo de especies a partir del índice Gini-Simpson o cualquier otra entropía generada con las fórmulas maestras mencionadas anteriormente. Todas llevan a una única fórmula maestra para el número efectivo de especies, expresado como una función del mismo parámetro q que nos dio el perfil de entropía de una comunidad; el parámetro q determina la sensibilidad del cálculo a la abundancia relativa de especies (Tabla 1). La gráfica del número efectivo de especies frente a q (donde q va desde cero a infinito) es el «perfil de diversidad» de la comunidad. Convertir todos los cálculos tradicionales de complejidad a una misma métrica sencilla, el número efectivo de especies, nos permite compararlos directamente para saber más sobre la estructura de una comunidad (Figura 1). Ya no estamos comparando el número de especies con el número de bits o con probabilidades, que era como comparar naranjas y manzanas. Y lo mejor de todo, cuando los cálculos tradicionales de complejidad, sensibles a la abundancia, se convierten al número efectivo de especies, obedecen al principio de replicación descrito anteriormente, como la riqueza de especies. Esto le proporciona algunas (aunque no todas) las propiedades intuitivas de la riqueza de especies. Por ejemplo, el número efectivo de especies permite medir la similitud entre comunidades observando la proporción de diversidad media intragrupal con la diversidad total agregada, la misma técnica que los biólogos (erróneamente) intentaban utilizar con los cálculos tradicionales. El buen desarrollo matemático que subyace al número efectivo de especies también revela cómo dividir la diversidad en componentes independientes intra e intergrupales, y muestra cómo estos componentes se relacionan con los cálculos habituales de similitud entre ecosistemas. El número efectivo de especies, por tanto, es la mejor herramienta para cuantificar el concepto de diversidad que utilizan realmente la mayoría de biólogos.

El concepto de diversidad se desarrolló para describir aspectos fundamentales de los ecosistemas. Sin embargo, para que la disciplina avance, el lenguaje descriptivo también debería conectar con la teoría predictiva. El concepto de diversidad en términos de número efectivo de especies tiene conexiones profundas con la mayoría de modelos importantes de ecosistema y población utilizados por los ecólogos, como el modelo neutral de Hubbell (2001). Los valores esperados de entropía generalizada y número efectivo de especies para q = 0, 1 y 2 son funciones analíticas simples de los parámetros fundamentales del modelo de Hubbell (Chao et al., 2015). Esto significa que los biólogos pueden predecir la diversidad y el parecido compositivo entre ecosistemas a partir de parámetros fundamentales como el tamaño de las poblaciones y la tasa de especiación, en el caso de modelos idealizados simples. Los biólogos todavía están muy lejos de poder predecir estas cuestiones en el desorden de los ecosistemas reales, pero este es un primer paso importante.

Ampliar el concepto de diversidad

¿Es perfecto este concepto de diversidad? Por supuesto que no. Una de las abstracciones subyacentes es que todas las especies son igual de diferentes unas de otras. Un grupo de cinco especies de rata tiene la misma diversidad que un grupo consistente en una rata, un armadillo, un manatí, un pangolín y un mono, siempre que las abundancias relativas sean iguales en ambos casos. Los cálculos de diversidad estándar dependen solo de las abundancias relativas de cada especie, no de su nivel de diferenciación. No obstante, el segundo grupo tiene mucha más historia evolutiva y, por lo tanto, mucho más valor de conservación. Con la aparición de las técnicas de secuenciación genética podemos calcular objetivamente el tiempo de divergencia entre especies, así que el concepto tradicional de diversidad, que era muy simple, se ha ampliado recientemente para incorporar la historia evolutiva única contenida en cada comunidad. Esto se hizo en un principio generalizando los métodos tradicionales –la riqueza de especies, la entropía de Shannon y, sobre todo, el índice Gini-Simpson– para incorporar el tiempo de divergencia, pero las generalizaciones de las dos últimas heredaron los mismos problemas de interpretación que sus progenitoras. Recientemente el marco entero de la diversidad entendido como número efectivo de especies, con todas sus divisiones y cálculos de similitud, se ha generalizado para incluir el tiempo de divergencia, y ahora hay una aproximación matemáticamente rigurosa dispuesta a enfrentarse a nuevas cuestiones ecológicas que hace unas décadas no podíamos ni imaginar (Chao, Chiu y Jost, 2010). También hay un trabajo continuado que intenta incluir las diferencias entre especies (véase Chao, Chiu y Jost, 2014), aunque estas diferencias son mucho más difíciles de cuantificar objetivamente que el tiempo de divergencia evolutiva.

«En modelos idealizados simples, los biólogos pueden predecir la diversidad y el parecido compositivo entre ecosistemas»

A pesar de estos avances en matemática de la diversidad, es esencial que nos demos cuenta de que la diversidad es solo un parámetro y de que el cuadro completo requiere parámetros descriptivos adicionales. Por ejemplo, la mayoría de los desarrollos hasta la fecha se han centrado en cálculos de la diversidad que dependen de las abundancias relativas. Estos cálculos funcionan bien para ecosistemas con densidades de individuos fijas, como el típico ecosistema boscoso en el que la composición de especies puede cambiar entre localizaciones o de un año a otro pero la densidad es más o menos estable. No obstante, en algunos ecosistemas la densidad total puede fluctuar rápidamente, como ocurre en algunas comunidades terrestres de insectos, que crecen brevemente con la aparición masiva de adultos voladores de especies de insectos acuáticos que proliferan en lagos aislados. Cuando se introduce una nueva especie superabundante en un ecosistema, los cálculos de diversidad sensibles a las abundancias caen drásticamente, porque se ven afectados por la equitatividad de la distribución de abundancias relativas. Esta disminución en diversidad (para q > 0) es una descripción exacta de la caída repentina en complejidad; ahora es muy probable que cualquier interacción entre dos individuos sea entre conespecíficos (de la especie superabundante), en lugar de entre dos especies distintas. Sin embargo, este no es el tipo de disminución de la diversidad que debería preocupar a los ecologistas. Para saber si deberíamos preocuparnos cuando disminuye la diversidad o no, necesitamos información adicional sobre las abundancias absolutas. En el caso de una invasión explosiva de insectos, la curva de acumulación de una especie (entendida como una función del trabajo de muestreo) nos dirá si hay algo de lo que preocuparse. La diversidad es un concepto poderoso, ¡pero no es lo único que tenemos que saber sobre un ecosistema!